

El COVID-19 llegó a México en el año 2020 cambiando drásticamente nuestras vidas. Desafortunadamente, las pruebas para la detección del COVID-19 son escasas en el territorio mexicano por lo que tenemos que hacer el mejor uso de ellas. En este artículo presentamos una parte de un modelo matemático de optimización combinatoria que determina la mejor distribución de los tests de COVID-19 en los diferentes municipios del país de tal manera que se cubra la mayor cantidad de gente. Consideramos el aspecto de la cobertura que corresponde a la población cubierta por tener cerca un hospital con pruebas COVID-19. El otro aspecto que consideramos es la accesibilidad que corresponde a la población que puede viajar hacia un hospital cercano con pruebas, en el caso de no tener un hospital que los cubra. Presentamos la solución del modelo implementado, tomando como ejemplo el estado de Chihuahua. Este trabajo es el resultado de una colaboración entre la Universidad de Edimburgo, el Tecnológico de Monterrey, el CINVESTAV y la empresa Logykopt.
Terminaba el 2019 y México cerraba un año más entre posadas, tamales, ponche, chocolate caliente y muchas otras festividades y comidas. Al mismo tiempo en Asia se desarrollaban acontecimientos que cambiarían drásticamente el curso del año 2020. Nos atrevemos a decir que la mayoría de los mexicanos estábamos ajenos e indiferentes a los sucesos que pasaban en aquel lejano continente. Y como cualquier otro año, inició el 2020 y conforme avanzaba se escuchaba cada vez con más fuerza el rumor de una enfermedad que ya no sólo atormentaba a la población asiática, si no a una parte de Europa, y que aún sin visualizarlo, dicha enfermedad se convertiría en protagonista y se llevaría miles de personas alrededor del mundo. El nombre de dicha enfermedad es COVID-19 (por sus siglas en inglés, Coronavirus Disease 2019) que apareció específicamente en Wuhan, China a finales del 2019 y que llegaría a México en los primeros meses del 2020.
Cuando la mayoría de los mexicanos nos dimos cuenta que esto era más grave de lo que pensábamos transcurría el mes de marzo y se presentaban los primeros casos en diferentes estados del país. Esos primeros casos se convertirían en millones al mes de diciembre y lamentablemente las muertes llegaron a los miles para dicho mes. México, al igual que todo el mundo se enfrenta a un gran reto en el que la ciencia y la tecnología serían unos aliados muy importantes.
En este artículo nos hacemos la siguiente pregunta: ¿cuál es la mejor forma de distribuir pruebas para la detección de COVID-19 a lo largo del territorio nacional tomando en cuenta a todas las personas en situación vulnerable? Otra pregunta podría ser, una vez creada la vacuna: ¿Cuál es la mejor manera de distribuir dicha vacuna en México? Las respuestas a estas preguntas pueden obtenerse haciendo uso de la Investigación de Operaciones (IO). Una excelente introducción al tema puede encontrarse en [HL02]. En pocas palabras y quedándose muy corta la definición, la IO es el área de las matemáticas que ayuda a los tomadores de decisiones a tomar las mejores decisiones apoyándose en diferentes técnicas tales como: el modelado matemático, el análisis estadístico y la optimización.
Para hacer uso del modelado matemático se requiere una pizca de creatividad, imaginación y ser muy apasionado. Normalmente, los modelos no quedan a la primera, hay que estarlos corrigiendo y mejorando. En este artículo, adaptamos un modelo matemático de cobertura que representa lo mejor posible cómo se llevaría acabo la asignación de pruebas para la detección de COVID-19 en los diferentes estados de la República Mexicana considerando a todas aquellas personas que no cuenten con un hospital COVID-19 cercano. Lo anterior se realiza con la finalidad de disminuir los casos de contagios e identificar los estados de la República Mexicana en situación crítica que requieren más pruebas de COVID-19. Hay que tomar en cuenta que el problema que abordamos en este trabajo pertenece a la clase de complejidad computacional NP-difícil [PS98].
Lo primero es identificar la información con la que se cuenta. En México, se tienen 2467 municipios agrupados en 32 estados. Además, podemos considerar la información que se muestra en la Figura 2.

Usamos dos conceptos muy importantes: el área de servicio y el área de movilidad. El área de servicio es un atributo de los hospitales y representa la cobertura que realiza un hospital a la redonda. Es decir, cuáles son los municipios que un determinado hospital puede cubrir a través de su área de servicio. Por otro lado, el área de movilidad es un atributo de los municipios y éste se refiere a la posibilidad que tiene la gente de un municipio para trasladarse a un hospital siempre y cuando dicho municipio no esté cubierto por el área de servicio de un hospital. Un ejemplo del área de servicio y del área de movilidad se muestra a continuación:
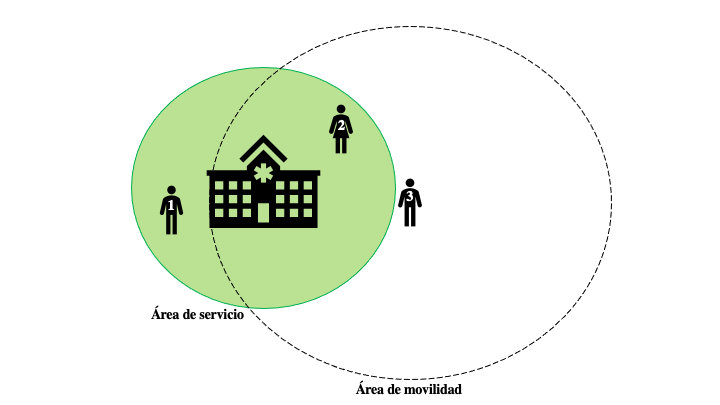
En la Figura 2, las siluetas representan los diferentes municipios. Como se observa, el municipio 1 y 2 están cubiertos por el área de servicio del hospital (área verde). Mientras que el municipio 3 no está cubierto pero puede acceder al hospital, ya que éste se encuentra dentro de su área de movilidad. Nosotros consideraremos los indicadores de accesibilidad basándonos en el artículo de O.J Ibarra-Rojas et al. titulado The maximal covering location problem with accessibility indicators [IOL20] pero adaptados al caso de asignación de pruebas COVID-19 en donde las variables de decisión más importantes son los hospitales a los cuales hay que asignarles pruebas de COVID-19. El modelo matemático que adaptamos toma en cuenta los siguientes indicadores:
Sea $I$ el conjunto de hospitales de los cuáles sólo $n$ podrán ser asignados con pruebas de COVID-19 ya que no todos pueden contar con insumos (vacunas o pruebas) al ser éstos muy limitados. El conjunto de los municipios de México es $J$. El conjunto $A(j)$ representa a los hospitales dentro del área de movilidad de cada municipio $j\in J$. Similarmente, $N(i)$ representa los municipios que el hospital $i\in I$ cubre. Una vez que se han definido los conjuntos anteriores, planteamos las variables de decisión del problema que en nuestro caso serán todas binarias: \begin{align*} z_i &= \begin{cases} 1, & \text{si al hospital $i \in I$ se le asignarán pruebas de COVID-19.}\\ 0, & \text{en otro caso.} \end{cases} \\ y_j &= \begin{cases} 1, & \text{si el municipio $j \in J$ está cubierto por algún hospital.}\\ 0, & \text{en otro caso.} \end{cases} \\ v_{ij} &= \begin{cases} 1, & \text{si el municipio $j \in J$ no está cubierto e $i \in I$ es el hospital con insumos más cercano.}\\ 0, & \text{en otro caso.} \label{eqns} \end{cases} \\ a_j &= \begin{cases} 1, & \text{si el municipio $j$ tiene acceso a un hospital con insumos.}\\ 0, & \text{en otro caso.} \end{cases} \end{align*}
Una vez definidas las variables de decisión definimos las restricciones. \begin{equation} \sum_{i \in I} z_i = n.\label{eq1} \end{equation}
La restricción \eqref{eq1} asegura que se abran exactamente $n$ hospitales. Recuerde que todas las variables de decisión que se definieron son binarias.
\begin{eqnarray} \sum_{i:j \in N(i)} z_i \leq My_j \quad j\in J, \label{eq4}\\ y_j\leq \sum_{i:j \in N(i)} z_i \quad j\in J. \label{eq5} \end{eqnarray} Las restricciones \eqref{eq4} y \eqref{eq5} ligan las variables de asignación con las de cobertura, en donde $M $ es un número muy grande. Si un municipio $j$ no está cubierto por algún hospital con pruebas de COVID-19 ($y_j=0)$, entonces ningún hospital $i\in I$ tal que $j\in N(i)$ tiene insumos ( $\sum_{i:j \in N(i)} z_i=0$). Por otro lado, si $\sum_{i:j \in N(i)} z_i=1$ nos indica que un hospital que cubre al municipio $j$ tiene insumos lo que obliga a $y_j=1$, es decir, el municipio está cubierto. \begin{eqnarray} v_{ij} \leq z_i \hspace{0.8 cm} i \in I, j \in J,\label{eq2}\\ \sum_{i \in I} v_{ij} = (1 - y_j) \hspace{0.8 cm} j \in J.\label{eq3} \end{eqnarray}
Las restricciones \eqref{eq2} y \eqref{eq3} ligan las variables $v_{ij}$ de proximidad con las de asignación de hospitales con las de cobertura de municipio. La variable $v_{ij}=1$ indica si el hospital $i$ en donde sí tienen pruebas de COVID-19 es el más cercano al municipio $j$ pero no lo cubre. Considere la restricción \eqref{eq2} y suponga que $z_i=0$, lo cual significa que el hospital $i$ no recibirá insumos. Por lo tanto, $v_{ij}$ debe ser cero, ya que el hospital $i$ más cercano al municipio $j$ debe tener insumos. Ahora, suponga que $z_i=1$, entonces, el hospital $i$ recibirá insumos. Por lo tanto, la variable $v_{ij}$ puede ser cero o uno; será cero, si el hospital $i$ no es el más cercano al municipio $j$ o que dicho municipio $j$ esté cubierto. Por otro lado, $v_{ij}$ será uno, cuando dicho hospital $i$ sea el más cercano al municipio $j$ y dicho municipio $j$ no este cubierto. Ahora, la restricción \eqref{eq3} obliga a las variables $v_{ij}$ a ser todas 0 si es que el municipio está cubierto por un hospital con insumos, es decir, si $y_j=1$. Se puede apreciar que las restricciones \eqref{eq2} y \eqref{eq3} son relativamente sencillas de expresar y nos ayudan a controlar la asignación de insumos en los hospitales. Ahora considere la siguiente restricción: \begin{eqnarray} a_j = y_j + \sum_{i \in A(j)} v_{ij} \hspace{0.8 cm} j \in J.\label{eq8} \end{eqnarray}
La restricción \eqref{eq8} nos permite saber si el municipio $j$ tiene acceso a la red de servicio. Es decir, nos indica si el municipio $j$ está cubierto o en su defecto tienen acceso a un hospital $i$ con insumos. Una vez definidas las restricciones (para este ejemplo sólo se ilustraron algunas restricciones) construimos la función objetivo del problema. En este ejemplo se tomarán dos de los indicadores ya antes mencionados:
Observe que el Indicador 1 ya se tiene representado mediante la variable de decisión $y_j$. Mientras que el Indicador 2, está representado por la variable de decisión $a_j$. Por lo tanto, la función objetivo quedaría de la siguiente manera:
\begin{equation} \text{max } \frac{1}{|J|} \sum_{j \in J} \left( w_1 a_j + w_2 y_j \right), \end{equation} donde $w_1$ y $w_2$ representan pesos que serán asignados por los tomadores de decisiones, $w_1,w_2 \in [0,1]$. En otras palabras, dichos pesos representan la importancia dada a cada indicador presente en la función objetivo. Además, se divide entre $|J|$ con la finalidad de mantener la función objetivo entre $[0,1]$. En este ejemplo, los tomadores de decisiones tomarán la decisión sobre qué es más importante, que un municipio $j$ se encuentre dentro del área de cobertura del hospital $i$ (Indicador 1) o que un municipio $j$ tenga acceso a la red de servicio, ya sea que esté cubierto por un hospital $i$ o pueda acceder a un hospital $i$ a través de su radio de movilidad (Indicador 2).
Considerando el escenario COVID-19, es posible añadir el índice de pobreza, la cantidad de contagios o la cantidad de muertes a la función objetivo. Se le da prioridad a aquellos indicadores que sean más importantes según los tomadores de decisión. Lo que se quiere es maximizar la cobertura, lo que se traduciría en llegar a todos aquellos municipios que se encuentran en situación vulnerable y realizar las pruebas necesarias para que los contagios disminuyan. Recuerde que se quiere cubrir a la mayor cantidad de municipios que sea posible y aquellos que estén cubiertos sean los más vulnerables. Un ejemplo de solución se muestra a continuación:
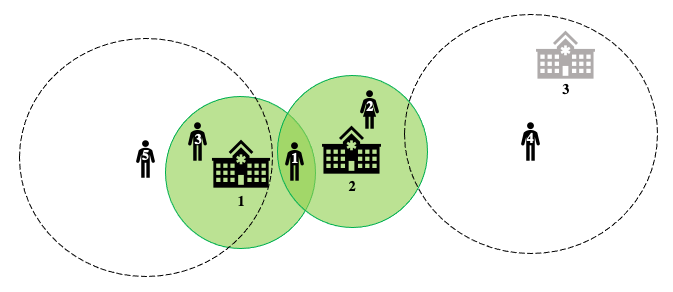
En la Figura 2, observamos cómo los hospitales 1 y 2 cuentan con insumos y éstos cubren a los municipios 1, 2 y 3 e incluso el municipio 1 está cubierto por dos hospitales lo que le da más opciones a elegir. Por otro lado, el municipio 5 no está cubierto pero debido a su radio de movilidad puede acceder al hospital 1. Finalmente, el municipio 4 no está cubierto ya que el hospital 3 no cuenta con insumos, y además no puede acceder a un hospital a través de su área de movilidad. La Figura 2 representa una situación real, debido a que los recursos son limitados, en este caso, las pruebas para la detección de COVID-19 son escasas, estas solo son asignadas a los hospitales que pueden cubrir a la mayor cantidad de municipios o que estos últimos puedan acceder a dichos hospitales. Si observa la Figura 2 no todos los municipios están cubiertos pero si lo están la mayoría de ellos y los que están cubiertos deben de ser los que tengan muchos contagios, una gran cantidad de muertes, sean municipios muy pobres o una combinación de todos.
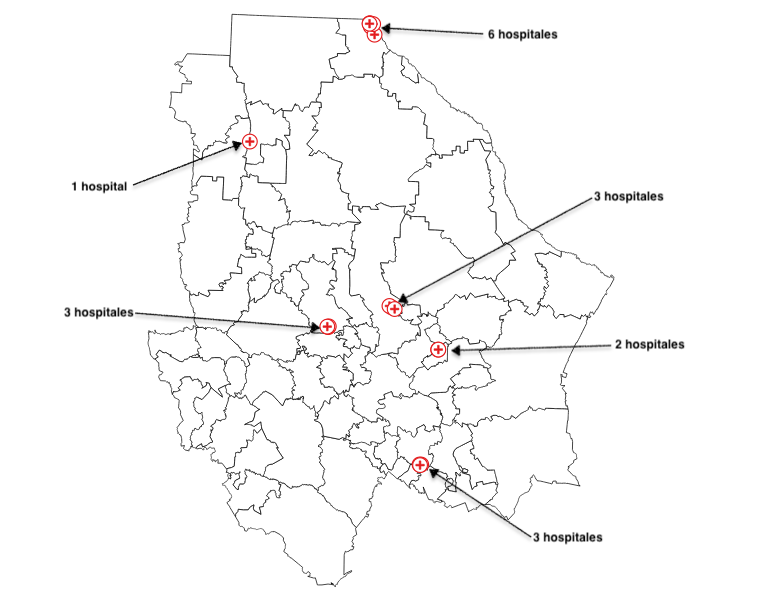
Por ejemplo, en el estado de Chihuahua tenemos un conjunto $I$ con 18 hospitales clasificados como COVID-19, dichos hospitales son representados en la Figura 2.1. En otras palabras, en todo el estado de Chihuahua existen solo 18 hospitales que pueden tener insumos para cubrir la demanda de los diferentes municipios. Sin embargo, se sabe que de esos 18 hospitales, solamente $n=6$ se les mandará insumos debido a las limitaciones. El número $n$ se calcula por la información periodística gubernamental acerca del número de pruebas y por la población actual en el estado de Chihuahua.
Cabe mencionar que el modelo presentado es una versión simplificada del que se puede encontrar en [IOL20]. Si se considera el modelo completo y tomando los indicadores enumerados previamente para el estado de Chihuahua, el modelo tendría 1,559 variables de decisión y aproximadamente 3,217 restricciones. Una vez completado el modelo, lo resolvemos mediante un algoritmo de ramificación y acotamiento [Wol98] que es una enumeración exhaustiva pero inteligente de todas las posibles soluciones posibles. Actualmente, existen varios paquetes informáticos (solvers) que utilizan lenguajes informáticos como C/C++ o Python para trasladar el modelo matemático a lenguaje informático y resolverlo. Un ejemplo de dichos paquetes informáticos son: Gurobi o CPLEX.
La Figura 2.1 muestra el resultado del modelo implementado para el estado de Chihuahua que cuenta con 67 municipios de los cuales 23 están cubiertos por algún hospital con pruebas COVID-19, 7 municipios pueden acceder a un hospital cercano y 37 se encuentran en situación vulnerable al no tener un hospital cercano con insumos.
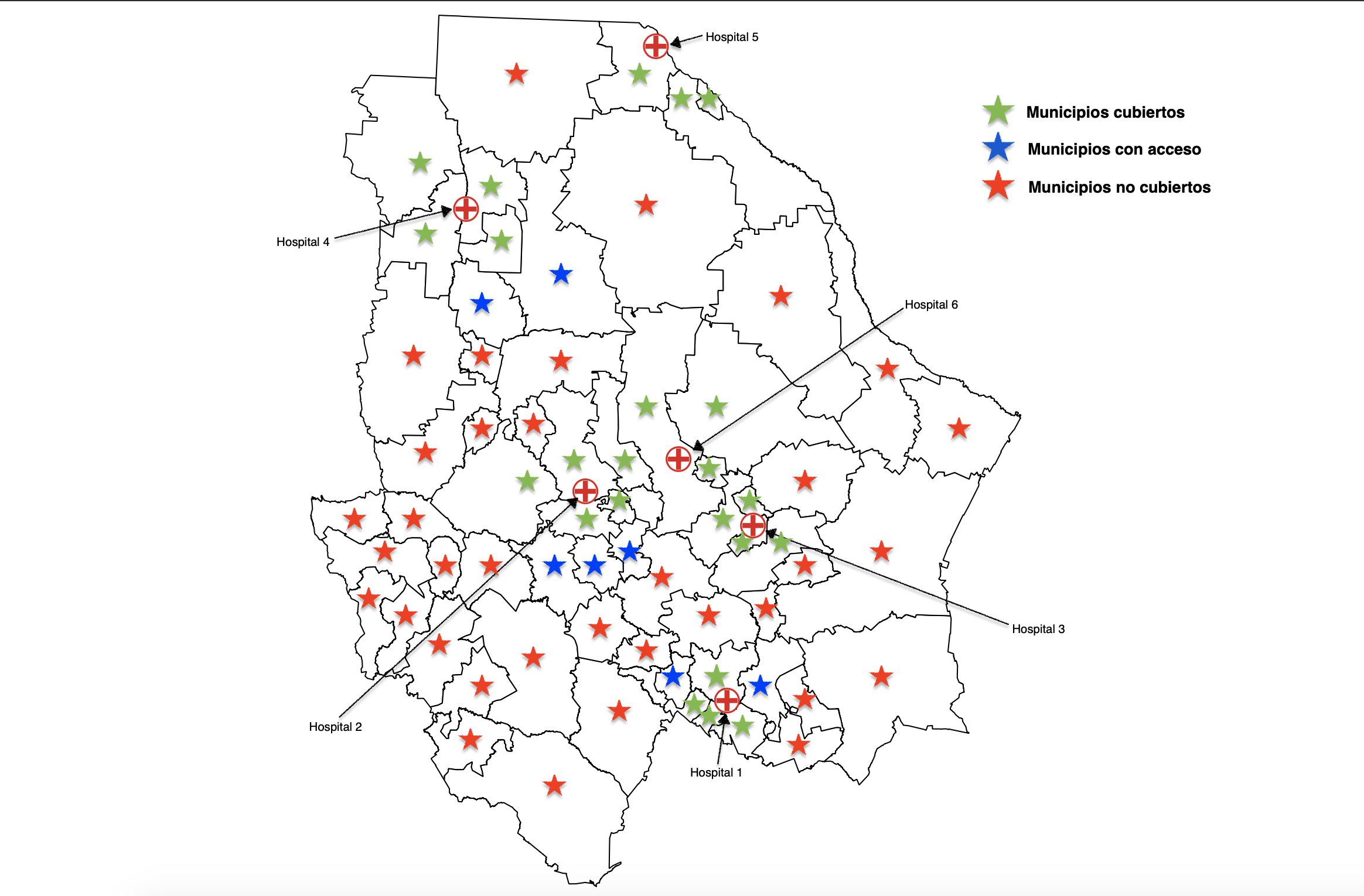
En general, un modelo matemático puede representar una situación del mundo real, la solución del modelo ayuda a los tomadores de decisiones a tomar una solución. El modelo puede ser tan complejo como uno quiera, ya sea agregando más variables de decisión, más restricciones o ambas. En general, entre más apegado sea a la realidad, los modelos suelen ser más complejos. La IO es una poderosa herramienta que en situaciones como la que se está viviendo puede ser de gran ayuda. También es importante mencionar que los paquetes informáticos mencionados tienen sus limitaciones. Por ejemplo, en este caso, resolver el modelo considerando a todo México (2467 municipios) es imposible ya que el modelo tiene muchas más variables y restricciones de la que un paquete informático puede manejar. Por lo tanto, es necesario la implementación de otras técnicas, tales como relajaciones, descomposiciones o metaheurísticas.
Este artículo fue escrito por el M. C. Salvador de Jesús Vicencio Medina como parte de su proyecto doctoral bajo la supervisión de la Dra. Yasmín Á. Ríos Solís, ambos asociados a la Escuela de Ingeniería y Ciencias del Tecnológico de Monterrey, Campus Monterrey. Dicho proyecto, inició con una colaboración entre la Universidad de Edimburgo, el Tecnológico de Monterrey, CINVESTAV y la empresa Logykopt a través de la convocatoria SFC-GCRF Covid-19
donde recibió el nombre de Optimal allocation of PCR and immunoassay tests of COVID-19 in Mexico and Ecuador. El resultado de la colaboración fue una herramienta que proporciona información sobre la vulnerabilidad, cobertura y accesibilidad de los diferentes Estados de la República Mexicana y que se puede consultar en el siguiente enlace http://logykopt-covid19.eastus2.cloudapp.azure.com/