

En 1948, el célebre matemático John von Neumann concibió la idea de los autómatas celulares (AC), al buscar resolver el problema de los sistemas auto-replicables. Su diseño inicial se basaba en la idea de un robot con la capacidad de construir a otro robot. Sin embargo, llevar a cabo este proyecto físicamente resultaba imposible, por lo que siguió el consejo de Stanislaw Ulam de desarrollar un modelo matemático discreto que pudiera replicarse a sí mismo [Neu66].
En el escenario clásico, un autómata celular es una transformación de una retícula regular $\mathbb{Z}^d$, donde cada célula de la retícula tiene un posible estado tomado de un alfabeto $A$. La característica clave de los autómatas celulares es que se definen mediante una regla local. Esta regla depende de un conjunto de memoria fijo y se aplica de manera simultánea a todas las células de la retícula.
Los autómatas celulares elementales (ACE) son autómatas celulares que admiten un conjunto memoria pequeño, el cual es $\left\{-1, 0, 1\right\}.$ Además, existen 256 ACE, los cuales son denominados como regla X
, donde $X$ es un entero entre 0 y 255.
En 1970, John Conway dió a conocer uno de los autómatas celulares de dos dimensiones más famosos, el Juego de la Vida, el cual resultó ser Turing completo, es decir, que puede simular una máquina de Turing universal.
La investigación en AC continuó evolucionando, y en 1983, Stephen Wolfram [Wol02] publicó un artículo donde presentaba su investigación computacional sobre las propiedades de los autómatas celulares unidimensionales. Entre sus experimentos, observó la evolución de una configuración aleatoria al aplicar de manera iterada un ACE con el objetivo de clasificar la complejidad de los ACE. Así definió cuatro clases de ACE, enumeradas en orden creciente de complejidad. Entre los ACE más importantes se encuentra la regla 110, pues Matthew Cook en [Coo+04] demostró que es un modelo Turing completo.
Recientemente, los trabajos de Ceccherini-Silberstein y Coornaert [CC10], entre otros autores, han enriquecido sustancialmente la teoría de los autómatas celulares a través del uso de herramientas de teoría de grupos, topología y sistemas dinámicos.
Una propiedad interesante, y poco estudiada, es que la composición de dos autómatas celulares siempre es un autómata celular. El objetivo de este artículo es presentar de forma intuitiva algunos conceptos relacionados con los autómatas celulares, y posteriormente, estudiar el comportamiento de la composición entre dos ACE. El primer resultado obtenido de este estudio es que la probabilidad de que la composición de dos ACE, tomados de forma aleatoria, sea nuevamente un ACE es de aproximadamente el 6.29%.
Más adelante, se presenta una clasificación de los ACE, basada en la complejidad del autómata celular en relación con su composición con otros ACE. Esta es una manera no trivial de agrupar los ACE que es diferente a la clasificación de Wolfram. Después se muestran todos los semigrupos (i.e. conjuntos cerrados bajo la composición) cuyos elementos son ACE y algunas de sus propiedades.
Un semigrupo se considera ACE-maximal si cumple con dos condiciones fundamentales: todos los elementos de $S$ son ACE y si $S'$ es un semigrupo donde todos sus elementos son ACE y $S\subseteq S'$, entonces $S=S'.$ En este estudio se concluyó que solo existen siete monoides ACE-maximales $M_i,$ $i=1,\ldots, 7$ (Lema 1).
La estructura de este artículo es la siguiente. En la sección 2 se introduce la definición de autómatas celulares y se explica detalladamente la composición de dos autómatas celulares elementales. En la sección 3 se describe el proceso de la clasificación de los ACE. Además, se introduce el concepto de autómata celular cuasi-elemental, que es un autómata celular unidimensional con conjunto memoria mínimo contenido en $\left\{k-1, k, k+1\right\}$ para algún $k\in \mathbb{Z}$. En la sección 4 se presentan algunos conceptos de teoría de semigrupos y se expone el resultado que establece que solo existen siete monoides ACE-maximales. Además se describen algunas propiedades que estos monoides cumplen. Finalmente, se presentan las conclusiones de este artículo, así como trabajo a futuro.
El siguiente texto y los resultados presentados ofrecen una perspectiva de los autómatas celulares sobre el grupo $\mathbb{Z}$, los cuales son conocidos como autómatas celulares unidimensionales. La teoría de autómatas celulares se puede generalizar a un grupo arbitrario $G$, para más información consultar [CC10].
Para definir un autómata celular, es necesario explicar algunos conceptos. El espacio de configuraciones es el conjunto $A^{\mathbb{Z}}$, donde los elementos son funciones con dominio $\mathbb{Z}$ y codominio un conjunto $A$, que se conoce como el alfabeto. Un elemento en $A^{\mathbb{Z}}$ puede verse como una sucesión bi-infinita: $$x=\dots ,x_{-2},x_{-1},x_0, x_1, x_2, \dots ,$$ donde $x_s:=x(s), \forall s\in \mathbb{Z}$. Este espacio se puede equipar con la topología producto de la topología discreta de $A$, conocida como topología prodiscreta.
La acción traslación o acción shift del grupo $\mathbb{Z}$ sobre $A^{\mathbb{Z}}$ se define para cada $k\in \mathbb{Z}$ y $x\in A^{\mathbb{Z}}$ mediante la función $(k\cdot x)(s):=x(s-k), \forall s \in \mathbb{Z}.$ La acción de traslación de $k\in \mathbb{Z}$ en $A^{\mathbb{Z}},$ simula trasladar una sucesión bi-infinita $k$ veces a la izquierda o derecha, dependiendo el signo, es decir,
$$k\cdot x= (\dots x_{-2-k }, x_{-1-k}, x_{-k} , x_{1-k}, x_{2-k},\dots ).$$
Con estos conceptos, se puede definir un autómata celular como sigue:
En otras palabras, un autómata celular está determinado por un subconjunto finito $S$ y una función local.
Un autómata celular elemental es un autómata celular $\mathcal{T}\colon \left\{0,1\right\}^{\mathbb{Z}}\rightarrow \left\{0,1\right\}^{\mathbb{Z}}$, cuyo conjunto memoria es $S=\left\{-1,0,1\right\}.$ En otras palabras, su regla local depende del estado de la célula actual y de sus vecinas izquierda y derecha.
Los autómatas celulares elementales se etiquetan como regla X, donde $X$ es un número entre 0 y 255. En cada caso, la regla local $\mu_X\colon A^S\rightarrow A$ está determinada como sigue: sea $X_1 \dots X_8$ la representación binaria de $X$ y se escriben los elementos de $A^S$ en orden lexicográfico decreciente, es decir, 111,110,$\dots$,000; entonces, la imagen del i-ésimo elemento de $A^S$ bajo $\mu_X$ es $X_i$.
En general, el conjunto memoria de un autómata celular no es único. Sea ${\mathcal{T}\colon A^\mathbb{Z}\rightarrow A^\mathbb{Z}}$ un autómata celular, $S$ el conjunto memoria de $\mathcal{T}$ y $\mu\colon A^S\rightarrow A$ su función local. Sea $S'$ un subconjunto finito de $\mathbb{Z}$ tal que $S\subseteq S'$. Entonces $\mathcal{T}$ también tiene a $S'$ como conjunto memoria con función local $\mu '\colon A^{S'}\rightarrow A$ definida como $\mu '(y)=\mu(y|_S)$ para toda $y\in A^S$. Sin embargo, todo autómata celular tiene un único conjunto memoria mínimo, el cual es la intersección de todos los conjuntos memorias admitidos por $\mathcal{T}$.
Como ejemplos de autómatas celulares elementales se tienen las reglas 12, 68 y 126, cuyas reglas locales se definen por medio de las tablas de la Figura 1. El primer renglón contiene a todos los elementos de $A^{\left\{-1, 0, 1\right\}}$ y el segundo renglón contiene a las imágenes $\mu(y)$ bajo la regla local, donde un cuadro en blanco representa un 0 y un cuadro en negro representa un 1.
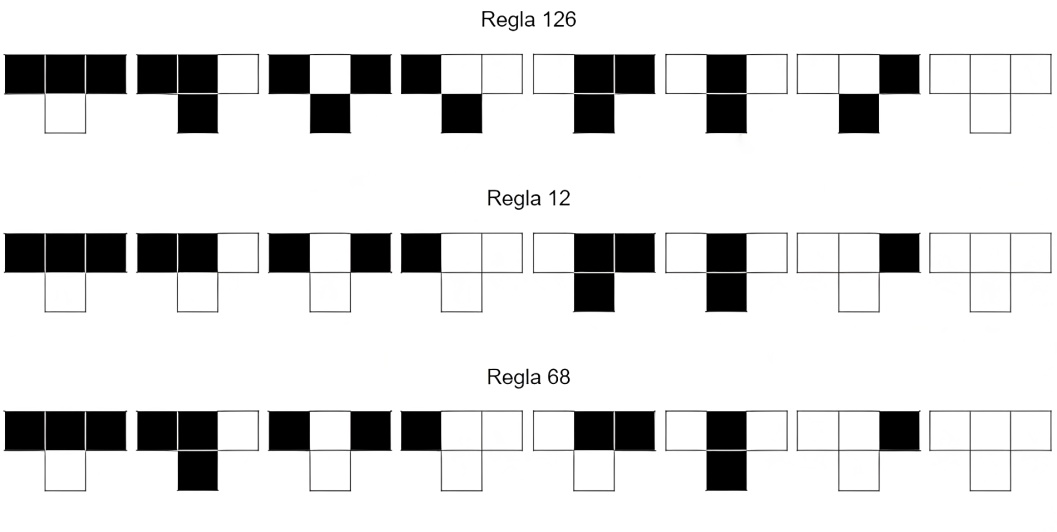
En concordancia con la nomenclatura, el segundo renglón de la tabla correspondiente a la regla 126 en la Figura 1 es 01111110, el cual, considerado como un número binario, corresponde al número decimal 126.
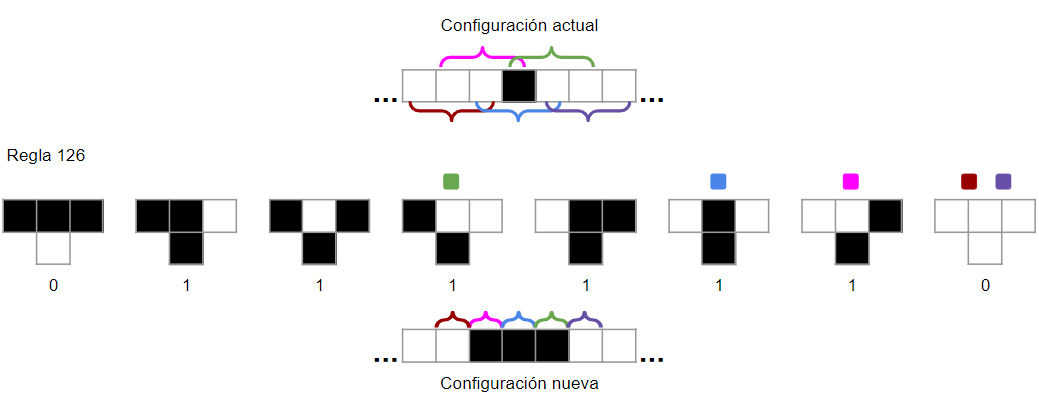
Ahora, en la Figura 2 se muestra cómo se aplica la regla 126 a una configuración en $A^{\mathbb{Z}}$, para ello se aplica de forma simultánea la regla local en cada elemento de la configuración. Por ejemplo, para conocer el estado del segundo cuadro blanco es necesario conocer el estado de sus vecinos y él mismo, lo cual se representa con el corchete rojo. Luego, se observa que para este elemento en la regla 126 corresponde el estado 0 o blanco y es por eso que el estado es blanco en el corchete rojo de la configuración nueva.
El siguiente resultado fue obtenido de [CC10], 1.4.9.
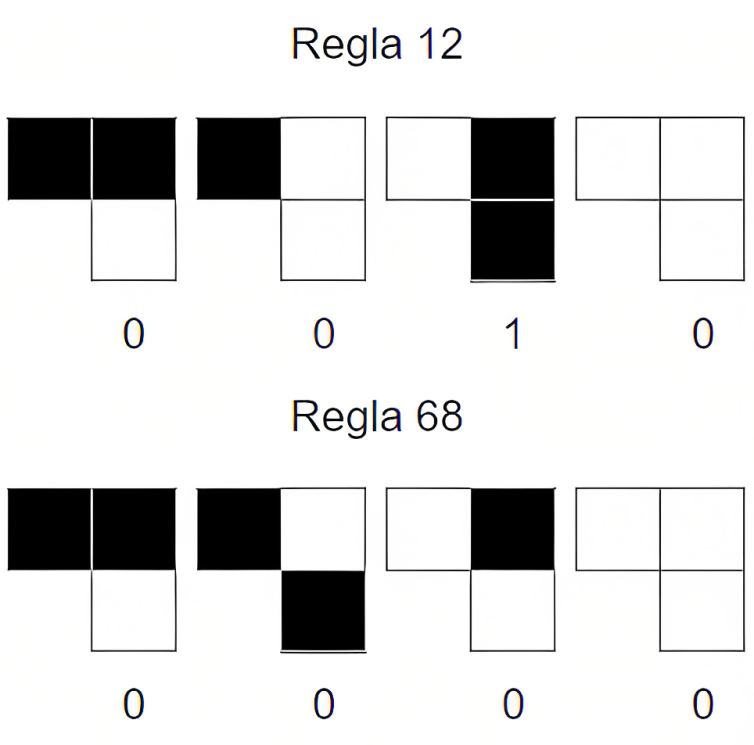
Sean $R_{12}$ y $R_{68}$ las reglas 12 y 68, respectivamente. Se ilustrará cómo se hace la composición de estas reglas. En las tablas de sus reglas locales, Figura 1, se observa que para $R_{12}$ el estado del vecino de la derecha no afecta al aplicar la regla, del mismo modo, para el vecino de la izquierda de $R_{68}$. Entonces sus conjuntos memoria mínimos son $S=\left\{-1,0\right\}, T=\left\{0,1\right\}$, y sus reglas locales, $\mu_{12}$ y $\mu_{68}$, están definidas por la tabla en la Figura 3.
Por el Teorema 1, un conjunto memoria de la composición es $$T+R=\left\{t+r: t\in T, r\in R\right\}=\left\{-1,0,1\right\}.$$ Entonces, al aplicar la composición $R_{68}\circ R_{12}$ a una configuración arbitraria ${\ldots x_{-2} x_{-1} x_0 x_1 x_2 \ldots \in A^{\mathbb{Z}} }$, se hace lo siguiente:
\begin{align*} R_{68}\circ R_{12}(\dots x_{-2} x_{-1} x_0 x_1 x_2\dots ) &= R_{68}(R_{12}(\dots x_{-2} x_{-1} x_0 x_1 x_2\dots ))\\ &= R_{68}(\dots \mu_{12}(x_{-2} x_{-1}) \mu_{12}(x_{-1} x_{0}) \mu_{12}(x_{0} x_{1})\dots ))\\ &= \dots \mu_{68}(\mu_{12}(x_{-1} x_{0}) \mu_{12}(x_{0} x_{1}))),\dots \end{align*}
Esto muestra que para saber cual será el valor de la composición en el elemento en la posición $x_i$, se observan los valores en $x_{i-1}, x_i, x_{i+1}$. Así el dominio de la regla local correspondiente a la composición $R_{68}\circ R_{12}$ es $A^{\left\{-1,0,1\right\}}$ debido a que $\left\{-1,0,1\right\}$ es un conjunto memoria de la composición.
En la Figura 4 se observa cómo hacer la tabla de la regla local de la composición $R_{68}\circ R_{12}$, donde se va aplicar el procedimiento anterior en cada uno de los elementos del dominio. Por ejemplo, recordando que se puede visualizar como 0 el cuadro en blanco y 1 el cuadro negro, en el tercer elemento del dominio, 101, se aplica $R_{12}$ en los primeros dos cuadros, 10, obteniendo 0 y luego en los siguientes dos cuadros, 01, obteniendo 1. Finalmente, se aplica $R_{68}$ al resultado obtenido anteriormente, 01, obteniendo 0. Este procedimiento se hace en cada uno de los ocho elementos del dominio, obteniendo finalmente la regla de la composición.

En resumen, la composición de autómatas celulares preserva la propiedad de ser un autómata celular, y un conjunto memoria, no necesariamente el mínimo, de la composición está dado por la suma de los conjuntos memoria de los autómatas celulares involucrados.
Ahora se continúa con el estudio de la composición de los autómatas celulares elementales, para ello se realizó la composición de los 256 autómatas celulares elementales entre sí, utilizando Python [Fou]. Con esta información, se calculó la probabilidad de que la composición de autómatas celulares sea elemental. Además, se determinó el número de autómatas celulares elementales que, al componerlos con cada autómata celular elemental, resultan en autómatas celulares elementales.
Para determinar si la composición de autómatas celulares es elemental basta ver que su conjunto memoria mínimo sea un subconjunto de $\left\{-1,0,1\right\}$. En a) de la Figura 5 se muestra una gráfica donde los puntos azules representan que la composición de la pareja de ACE es elemental, mientras que los puntos blancos indican que la composición no es elemental. Se observa que al componer las reglas ${0,51,204,255}$ siempre se obtienen ACE.
Dado que la definición de ACE es demasiado rígida, en el sentido que no se permite que se traslade el conjunto memoria, se define lo siguiente. Un autómata celular unidimensional es cuasi-elemental si su conjunto memoria está contenido en el conjunto $\left\{k-1, k, k+1\right\}$ para algún $k\in \mathbb{Z}$. En otras palabras, son autómatas celulares elementales pero con el conjunto memoria trasladado. Entonces, para determinar si la composición de autómatas celulares es cuasi-elemental, basta ver que su conjunto memoria mínimo está contenido en el conjunto $\left\{k-1, k, k+1\right\}$ para algún $k\in \mathbb{Z}$.
De las $256^2$ composiciones realizadas, ahora se seleccionaron aquellas que son cuasi-elementales. En la b) de la Figura 5 se muestra una gráfica donde los puntos azules indican que la composición de la pareja de autómatas celulares elementales es cuasi-elemental, mientras que los puntos blancos señalan que la composición no es cuasi-elemental. Se observa que al componer las reglas ${0,15,51,85,170,204,240,255}$ siempre se obtienen autómatas celulares cuasi-elementales.
|
|
|
| a) Composiciones elementales se muestran en azul y no elementales en blanco. | b) Composiciones cuasi-elementales se muestran en azul y no cuasi-elementales en blanco. |
Con base en la información anterior, se calculó que la probabilidad de que la composición de dos ACE, arbitrarios tomados al azar, sea un ACE es aproximadamente del 6.29%. Si se excluyen las reglas $0, 51,204$ y 255, la probabilidad de obtener una composición elemental se reduce al 3.3%. Por otro lado, la probabilidad de que la composición de dos ACE, arbitrarios tomados al azar, sea un autómata celular cuasi-elemental es aproximadamente del 11.79%. Si se excluyen las reglas $0, 51, 170, 204, 240$ y 255, la probabilidad de obtener una composición cuasi-elemental se reduce al 7.5%.
Un autómata celular elemental $\sigma$ es compañero izquierdo de $\tau$ si $\sigma\circ\tau$ es elemental. Del mismo modo, $\sigma$ es compañero derecho de $\tau$ si $\tau\circ\sigma$ es elemental.
Similarmente, se define el concepto de compañero izquierdo cuasi-elemental y compañero derecho cuasi-elemental de un autómata celular elemental $\tau$.
Con base en esta información, se clasificó qué tan complejo es un autómata celular elemental con respecto a la composición del autómata celular con otros, es decir, la relación entre el número de compañeros izquierdos y derechos. Para ello, se utilizó la paquetería de Python scipy.cluster.hierarchy, que es un método de agrupación jerárquica. Más información sobre la paquetería se puede consultar en [com22], y sobre el método, en [Nie16].
El conjunto de datos que se usó se explica a continuación. A cada uno de los 256 autómatas celulares elementales se le asignó un punto en el espacio donde la primera entrada corresponde al número de compañeros izquierdos y la segunda entrada al número de compañeros derechos. Además, la distancia que se implementó fue la distancia euclidiana.
Para medir qué tan buena es nuestra agrupación se usa el coeficiente de silueta, cuyo rango de valores es de -1 a 1. Si es 1, representa que los grupos están bien separados entre sí y hay una clara diferencia entre los grupos. Si es 0, la distancia entre los grupos no es significativa. Finalmente -1 significa que los grupos están mal asignados. Para más información consultar [Bha20].
Primero se hizo el análisis para el número de compañeros elementales y después para el número de compañeros cuasi-elementales. Se hace una distinción ya que, en los compañeros elementales se está clasificando a los autómatas celulares elementales en donde el conjunto memoria mínimo de la composición con otros no crece ni se traslada. Por otro lado, en los compañeros cuasi-elementales el conjunto memoria mínimo de la composición con otros no crece pero se permite que se traslade.
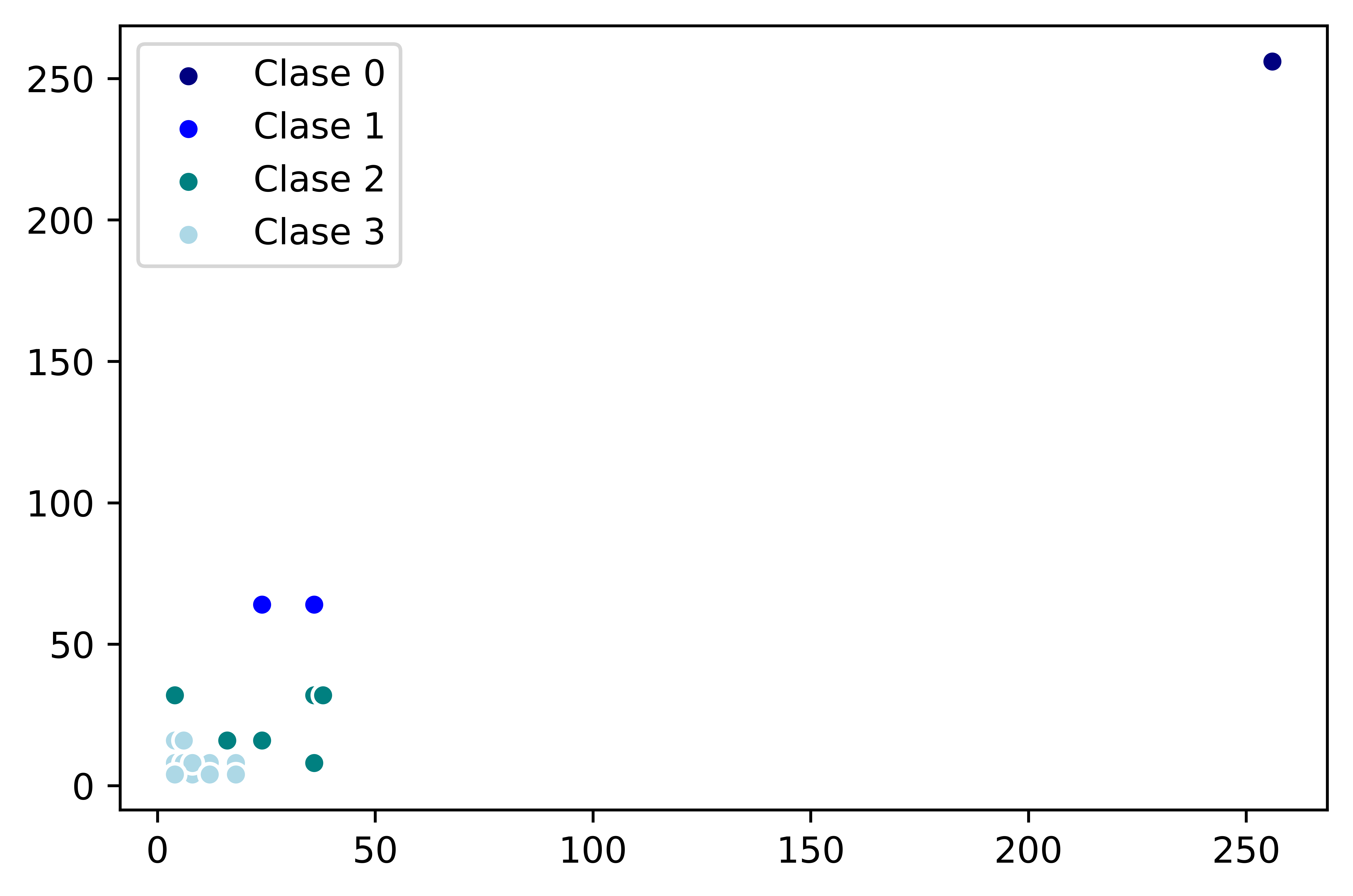
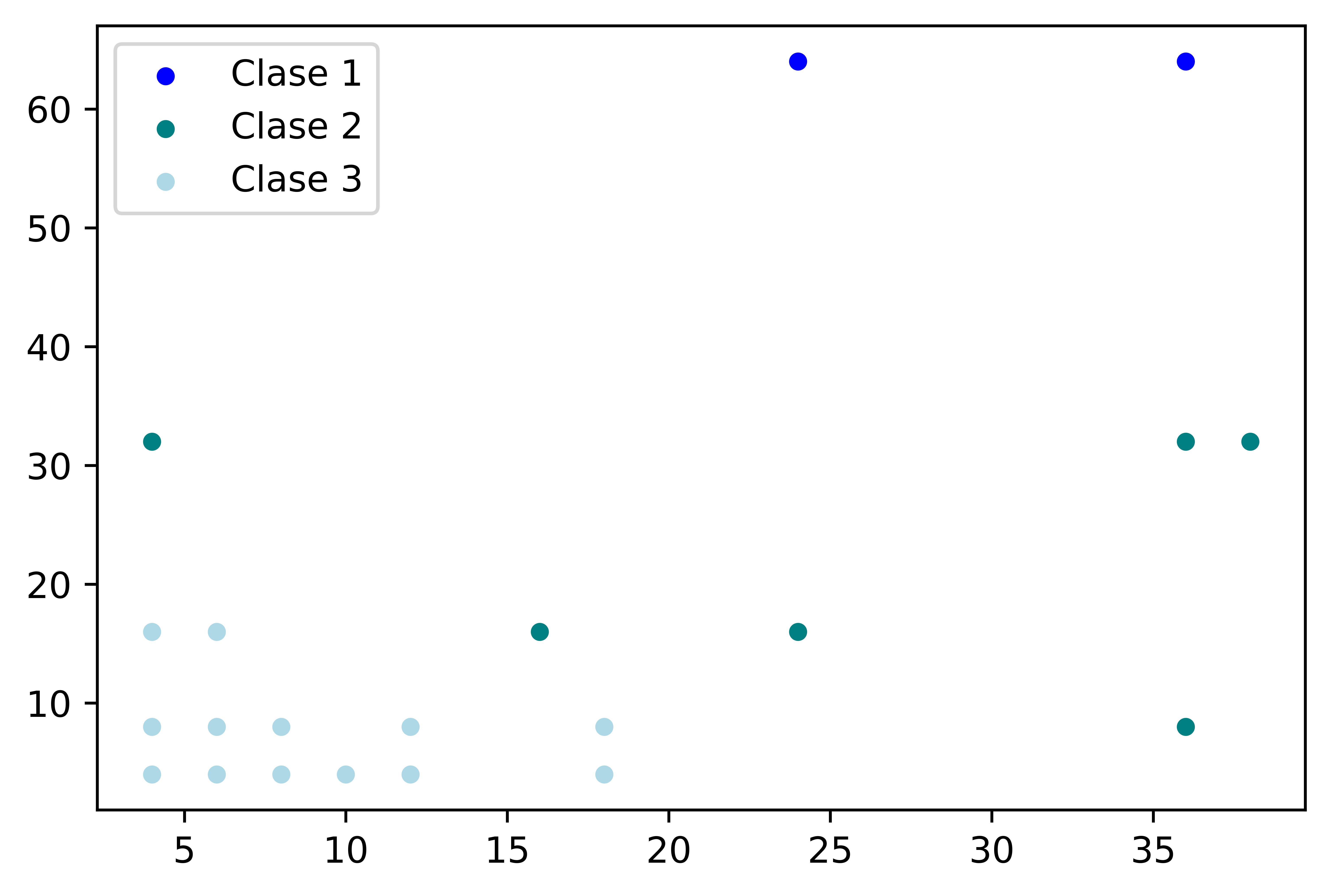
Se utilizaron los datos del número de compañeros graficados en la Figura 6, y se calculó el coeficiente de silueta para determinar qué tan buena es la agrupación. Con 4 grupos, se obtuvo un coeficiente de silueta de 0.7058, por lo que se eligieron 4 grupos para clasificar a los autómatas celulares elementales, los cuales se observan en la Figura 6.
|
|
|
| Clasificación por número de compañeros | Clasificación por número de compañeros sin la clase 0 |
En la clase 0 están los ACE cuyos compañeros son los 256. La clase 1 contiene a aquellos con 64 compañeros derechos y 36 ó 24 compañeros izquierdos. La clase 2 incluye a los ACE con un máximo de 38 compañeros, ya sea en el número de compañeros izquierdos, derechos o ambos. La clase 3 está compuesta por ACE con menos compañeros, con un máximo de 18 compañeros izquierdos, derechos o ambos.
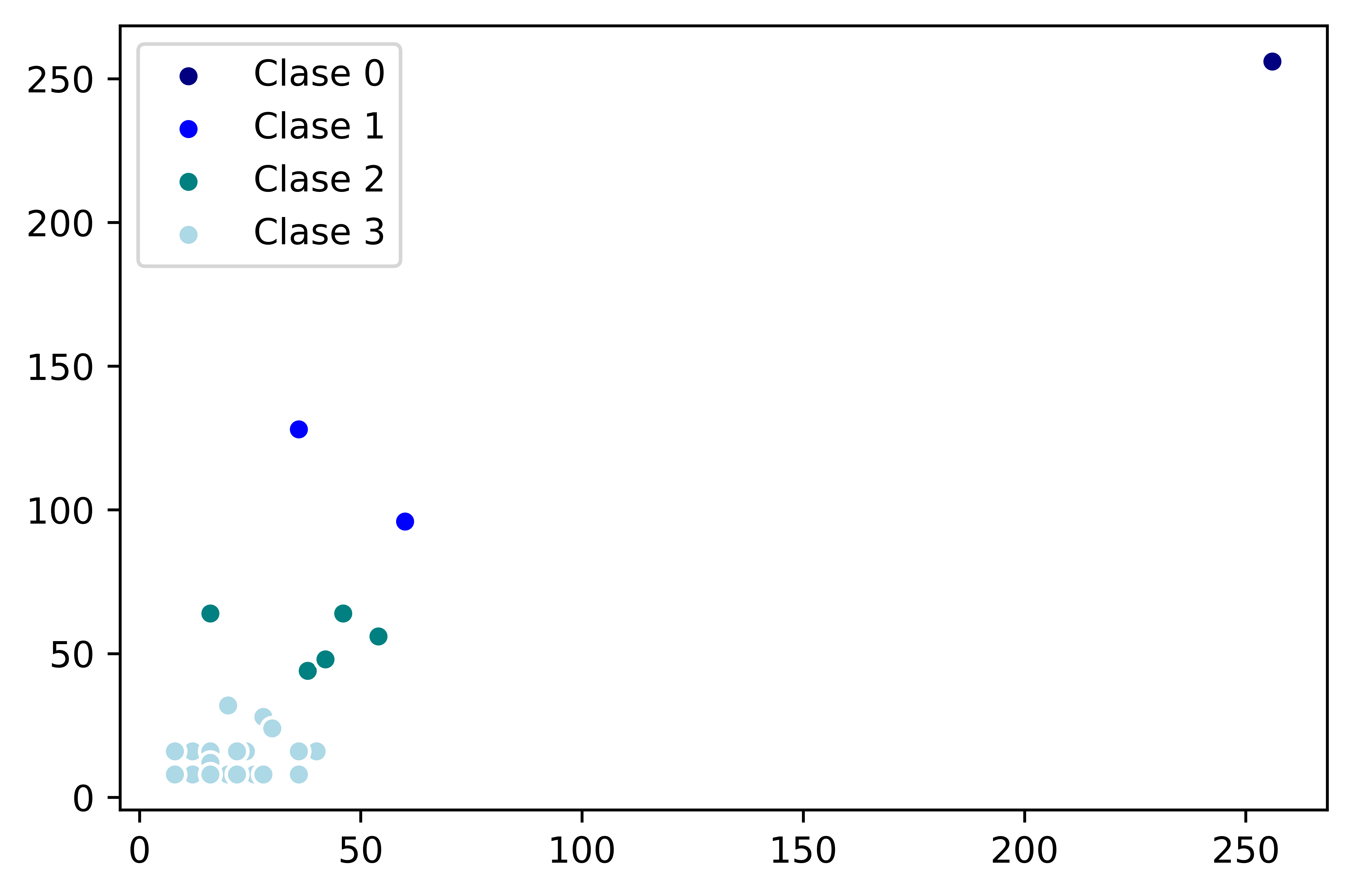
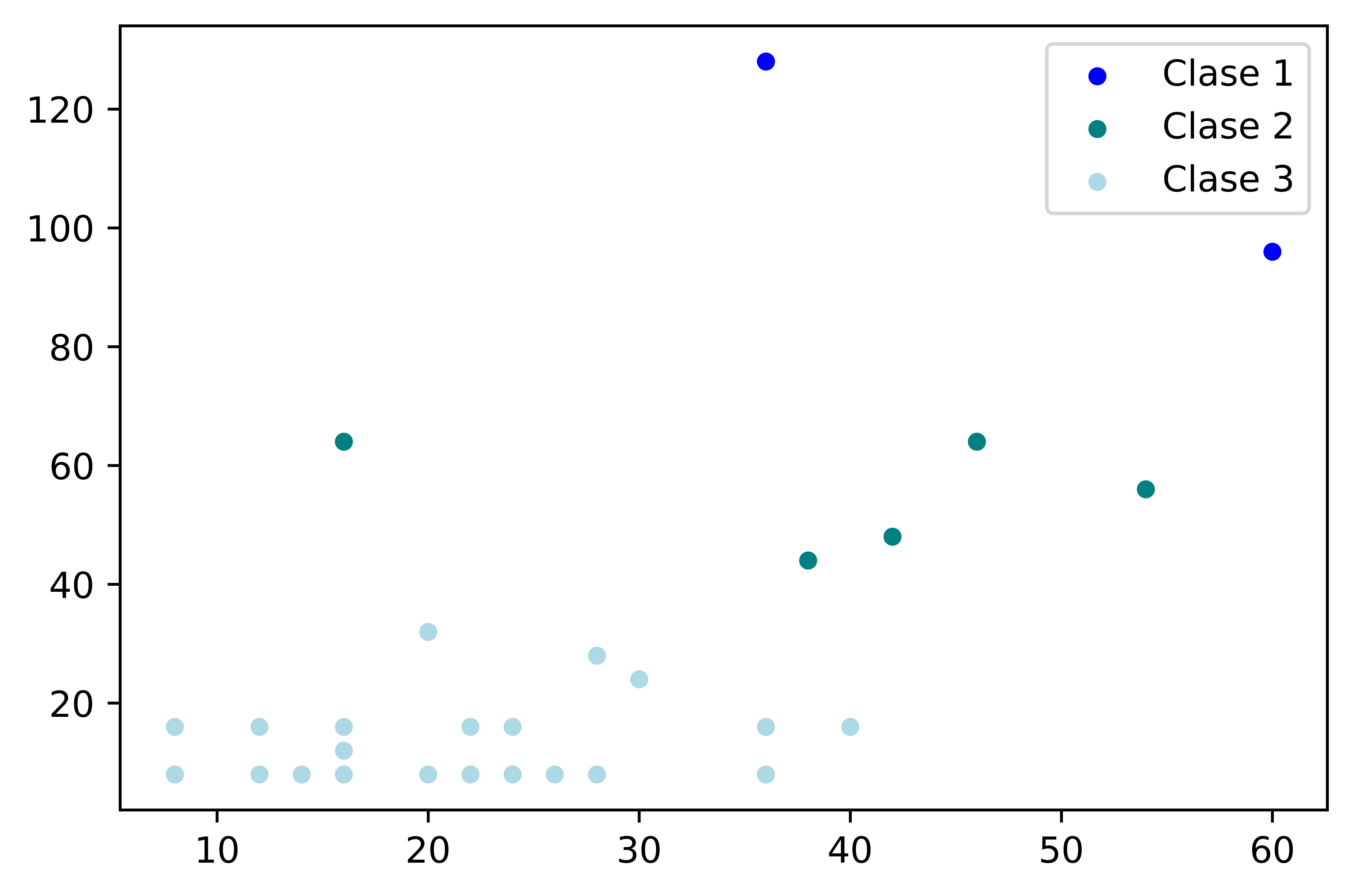
Posteriormente, se realizó el análisis con los datos del número de compañeros cuasi-elementales. Con 4 grupos, se obtuvo un coeficiente de silueta de 0.7281, por lo que se eligieron 4 grupos para clasificar a los autómatas celulares cuasi-elementales. En la Figura 7 se observa una gráfica de los ACE divididos en las 4 clases.
En la clase 0 están los autómatas celulares elementales cuyos compañeros cuasi-elementales son los 256. La clase 1 incluye a aquellos con 128 ó 96 compañeros cuasi-elementales derechos y 36 ó 60 compañeros cuasi-elementales izquierdos. La clase 2 está compuesta por ACE con un máximo de 64 compañeros cuasi-elementales, ya sea en el número de compañeros cuasi-elementales izquierdos, derechos o ambos. La clase 3 contiene a los ACE con menos compañeros cuasi-elementales, con un máximo de 40 compañeros cuasi-elementales izquierdos, derechos o ambos.
|
|
|
| Clasificación por número de compañeros cuasi-elementales | Clasificación por número de compañeros cuasi-elementales sin la clase 0 |
En el Cuadro 1 se muestran los autómatas celulares elementales que pertenecen a cada una de las 4 clases obtenidas con el agrupamiento jerárquico usando los compañeros cuasi-elementales. En el cuadro no aparecen explícitamente los 256 ACE, pues los ACE que no aparecen pueden obtenerse aplicando algunos automorfismos (ver [Mag23] para más información sobre estos automorfismos). Además, se muestra el total de ACE en cada clase.
| Clase | Total | Reglas | |||||
| Clase 0 | 8 | 0 15 51 170 204 | |||||
| Clase 1 | 16 | 2 8 12 34 | |||||
| Clase 2 | 28 | 3 4 14 19 24 32 42 136 200 | |||||
| Clase 3 | 204 |
|
Se comenzará definiendo algunos conceptos básicos de teoría de semigrupos.
Las relaciones de Green se volvieron muy importantes en el estudio de la teoría de semigrupos, para definirlas es necesario explicar los siguientes conceptos.
Una vez que se analizaron las composiciones de autómatas celulares elementales, se buscaron conjuntos de autómatas celulares elementales que, al componerlos entre sí, resultaran en algún elemento del mismo conjunto. Es decir, conjuntos cerrados bajo la composición. Dado que la regla 204 es la identidad y forma parte de esos conjuntos, entonces se obtendrán monoides de autómatas celulares elementales.
Un semigrupo $S$ se denomina ACE-maximal si satisface dos condiciones:
Por la cerradura de la operación, un monoide $S$ ACE-maximal debe satisfacer que $X^2\in S$ para toda $X\in S.$ Para encontrar los monoides ACE-maximales se considera el conjunto $$Q=\left\{X : X\circ X \text{ es un ACE } \right\}.$$ Realizando cálculos directos, se obtiene: $$Q=E\cup\left\{8, 51, 64, 239, 253\right\}.$$
El siguiente lema caracteriza los monoides ACE-maximales, su demostración puede verse en [CM23].
Resulta que el monoide $M_1$ es isomorfo a $M_2$, $M_3$ es isomorfo a $M_4$ y $M_6$ es isomorfo a $M_7,$ por lo que se continuará estudiando solo a los monoides $M_1, M_3, M_5$ y $M_6.$ A continuación en las Figuras 8, 9 y 10 se presentan las tablas de Cayley de estos monoides.
| $M_1$ | 0 | 4 | 8 | 12 | 64 | 68 | 200 | 204 | 255 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 0 | 4 | 8 | 12 | 64 | 68 | 0 | 4 | 0 |
| 8 | 0 | 0 | 0 | 0 | 0 | 0 | 8 | 8 | 0 |
| 12 | 0 | 4 | 8 | 12 | 64 | 68 | 8 | 12 | 0 |
| 64 | 0 | 0 | 0 | 0 | 0 | 0 | 64 | 64 | 0 |
| 68 | 0 | 4 | 8 | 12 | 64 | 68 | 64 | 68 | 0 |
| 200 | 0 | 0 | 0 | 0 | 0 | 0 | 200 | 200 | 255 |
| 204 | 0 | 4 | 8 | 12 | 64 | 68 | 200 | 204 | 255 |
| 255 | 255 | 255 | 255 | 255 | 255 | 255 | 255 | 255 | 255 |
|
|
A diferencia de los monoides anteriores que solo tienen a la identidad como elemento invertible, $M_5$ tiene dos elementos invertibles la regla 51 y la identidad.
| $M_5$ | 0 | 51 | 204 | 255 |
| 0 | 0 | 0 | 0 | 0 |
| 51 | 255 | 204 | 51 | 0 |
| 204 | 0 | 51 | 204 | 255 |
| 255 | 255 | 255 | 255 | 255 |
Por otro lado, se observó que los monoides $M_1, M_3$ y $M_6$ son $H-$triviales, es decir, que la relación $H$ de Green es trivial, y los monoides $M_3$ y $M_6$ son $L-$triviales, es decir, que la relación $L$ de Green es trivial. Posteriormente, se encontró que los monoides $M_3,$ $M_6$ y $M_{1b}=\left\{0,4,204,255\right\}$ son bandas regulares y bandas regulares izquierdas. También se analizó el submonoide $M=M_1-\left\{255\right\}$ de $M_1$, el cual es un monoide con cero, reversible derecho y R-trivial.
Las bandas regulares izquierdas son utilizadas por Brown [Bro00] para analizar random walks o paseos aleatorios. Por otro lado, en [Ayy+15], desarrollan una teoría general de las cadenas de Markov realizables como paseos aleatorios en monoides R-triviales.
Este artículo se centró en los autómatas celulares elementales, los cuales son un conjunto finito de reglas sencillas, lo que permite un enfoque computacional y la obtención de resultados algebraicos. Entre estos resultados, se destacan la clasificación de los 256 autómatas celulares elementales en 4 clases, basada el número de compañeros izquierdos y derechos. Esta clasificación mide la complejidad de un ACE con respecto a su composición con otros ACE.
Además, se presentó que cualquier semigrupo de ACE debe estar contenido en uno de los 7 monoides $M_1, M_2, M_3, M_4, M_5, M_6$ o $M_7.$ Adicionalmente, los monoides $M_3$ y $M_6$ son bandas regulares izquierdas, las cuales son usadas para estudiar paseos aleatorios. Por otro lado, el submonoide $M$ es un monoide R-trivial, los cuales tienen aplicaciones en el análisis de cadenas de Markov.
Este artículo está basado en la tesis de maestría [CM23] de la autora, la cual fue escrita bajo la supervisión del Dr. Alonso Castillo Ramírez, en el Centro Universitario de Ciencias Exactas e Ingenierías de la Universidad de Guadalajara. Como trabajo a futuro, se propone seguir ampliando este estudio, generalizando los resultados obtenidos durante la maestría [CM23], para incluir autómatas celulares unidimensionales con un alfabeto de 3 elementos, así como autómatas celulares de dos dimensiones, lo que plantea nuevos desafíos computacionales.