

En este artículo se reseña una teoría de la enseñanza de las matemáticas (APOE), presentando sus características principales y su uso en el diseño de actividades y material didáctico. En particular hacemos referencia a cómo ha sido aplicada con éxito en varios cursos de álgebra lineal.
Desde hace un poco más de diez años, se ha venido desarrollando en el Instituto Tecnológico Autónomo de México una serie de investigaciones en el área de educación matemática sobre la enseñanza del álgebra lineal usando una teoría del aprendizaje llamada APOE. Esta teoría tiene sus raíces en el trabajo de Jean Piaget y fue desarrollada inicialmente en 1980 por el profesor Ed Dubinsky [Arn+14] como un esfuerzo por estudiar y comprender el aprendizaje de las matemáticas. El nombre de la teoría APOE viene del acrónimo de Acción, Proceso, Objeto y Esquema que son las estructuras mentales que la conforman. Esta teoría constructivista se ha usado extensamente en los últimos cuarenta años con buenos resultados cuando, con base en ella y a partir de los resultados de investigación, se utiliza para diseñar actividades eficaces para la enseñanza de las matemáticas.
Las artículos de investigación y materiales desarrollados por los profesores incluidos en éste proyecto se han enfocado principalmente en los temas del primer curso de álgebra lineal a nivel licenciatura, que es de suma importancia para el currículo de un matemático aplicado. A lo largo de una década, se han desarrollado materiales didácticos para casi todos los temas del curso (ver por ejemplo [DTA08] [FPT18] [Tri13] [TP13]). En el caso de la enseñanza del álgebra lineal, casi todas las actividades han sido formuladas en términos de problemas de modelado. porque además de motivar el interés, son compatibles con la teoría APOE que los utiliza como una herramienta para la construcción de estructuras mentales. Se ha encontrado que usar estos problemas permite que los estudiantes desarrollen paulatinamente las habilidades de abstracción necesarias para construir los objetos matemáticos. Además, está bien documentado que su uso crea la necesidad en el alumno de definir los conceptos y herramientas del álgebra lineal de manera autónoma para trabajar con el modelo (ver [ST15] [TP13]), por lo que estamos convencidos que esto resulta en un aprendizaje más significativo en los estudiantes, que otros métodos tradicionales de la enseñanza de las matemáticas.
Uno de los pilares de la teoría es el diseño de descomposiciones genéticas, que son modelos cognitivos en los que se explica cómo los individuos construyen su conocimiento sobre los conceptos matemáticos. Gracias a éstas, la teoría APOE no sólo es una teoría abstracta, sino que puede ser llevada a la prárctica: un profesor, mediante una descomposición genética, puede diseñar actividades que busquen promover la construcción de las estructuras requeridas en el aprendizaje de un concepto que prevé la descomposición. El desarrollo cognitivo que tengan los alumnos en el momento de resolver las actividades, sus dificultades y sus dudas conforman una medida confiable sobre la bondad de la descomposición genética y de las actividades diseñadas, que en ese momento pueden ser retroalimentadas, evaluadas y replanteadas para ser más efectivas.
A continuación, se describirá brevemente la teoría de una forma introductoria con ejemplos muy concretos, que nos ayudarán a ilustrar el sabor del trabajo que se realiza al investigar con este marco teórico. La teoría APOE es compleja y extensa, si el lector se interesa en profundizar en sus fundamentos, recomendamos leer [Arn+14] que fue publicado en 2014 por Dubinsky y sus colaboradores como una guía para usar y entender la teoría.
Los pilares de la teoría APOE son cuatro construcciones mentales: Acción, Proceso, Objeto, y Esquema; llamadas concepciones cuando el estudiante muestra evidencia de ellas al resolver distintos problemas o al responder varias preguntas. Haremos un recorrido ilustrando las cuatro y los mecanismos mentales necesarios para construirlas.
Acción: Transformación del objeto matemático que el estudiante percibe como externo. Puede ser, por ejemplo, la implementación paso a paso de un algoritmo siguiendo instrucciones específicas o la verificación de que un objeto particular cumple con una definición o tiene una propiedad. Las acciones son la base de la teoría pues son necesarias para desarrollar las otras estructuras.
Ejemplos:
Como podemos observar, las acciones son necesarias y pueden ser simples o complicadas según el contexto. Sin embargo, un estudiante que está limitado a realizar acciones no podrá trabajar de manera adecuada, por ejemplo en la composición de funciones o en la modelación de un problema. A medida que las acciones se repiten y el estudiante reflexiona sobre ellas, dejan de ser externas para el estudiante y se vuelven internas. El estudiante puede entonces anticiparse al resultado de realizarlas, también se vuelve capaz de revertirlas. Al mecanismo que, mediante la reflexión, convierte a las acciones en algo que el estudiante reconoce como interno se le llama interiorización y a la construcción mental que se obtiene se le llama proceso.
Proceso: Construcción interna que ejecuta las acciones que le dieron origen pero que no está dirigido por estímulos externos. El individuo es capaz de anticipar el resultado de una acción sin tener que realizarla explícitamente o puede revertir el proceso en la acción o acciones correspondientes.
Ejemplos:
Los procesos se pueden coordinar con otros procesos para crear nuevos procesos.
Ejemplos:
El mecanismo mental para construir un objeto a partir de los procesos es la encapsulación. Se logra a través de la reflexión del estudiante para entender un proceso como un ente al que se le pueden aplicar acciones.
Objeto:Proceso que se entiende como un ente al que se le pueden aplicar nuevas acciones, no sólo las que le dieron origen, entonces decimos que el proceso se ha encapsulado como un objeto cognitivo.
Ejemplo:
Finalmente, la última construcción mental son los Esquemas, que como veremos a continuación son la parte más rica para indagar en los estudiantes que ya han terminado el curso.
Esquemas: Colección de posibles acciones, procesos, objetos y otros esquemas que están relacionados de forma coherente entre sí y que el estudiante puede evocar (de forma consciente o inconsciente) en la solución de un problema matemático.
Ejemplo:
Notemos que los esquemas son personales y corresponden a una estructura dinámica que cambia constantemente mediante el uso de sus componentes en la solución de problemas. La dinámica de los esquemas puede describirse por medio de su desarrollo. Dos estudiantes que han terminado un curso introductorio de álgebra lineal podrían en principio tener dos esquemas totalmente distintos. La descripción de los niveles de desarrollo de los esquemas en la teoría es más intrincada pero a grandes razgos se puede describir de la siguiente manera:
Los niveles de desarrollo del esquema se identifican por el tipo de relaciones construidas entre los componentes del esquema. El nivel Intra se caracteriza porque algunos de ellos están relacionados entre sí mientras que otros se encuentran asilados, pero el estudiante los relaciona con el mismo tipo de problema. En el nivel Inter se construyen relaciones fuertes entre los componentes del esquema, se identifican transformaciones y se comienzan a formar grupos de estructuras. En el nivel Trans, aparecen relaciones de conservación y la posibilidad de explicitar las relaciones; el esquema se vuelve coherente y puede ser tematizado para convertirlo en un nuevo objeto.
El estudio usando APOE se basa en el planteamiento de una descomposición genética que es un modelo hipotético de las estructuras mentales y los mecanismos que se piensa son necesarios en el aprendizaje de un concepto matemático o de un tema. Las descomposiciones genéticas sirven como hipótesis que pueden ser probadas experimentalmente a partir de diseños de enseñanza basados en ella y que típicamente irán cambiando y reformándose con la retroalimentación de las dificultades y éxitos de los estudiantes al seguir esos diseños.
La descomposición genética permite a los investigadores y a los profesores crear actividades más finas, con un mayor nivel de detalle, que promuevan las construcciones del estudiante.
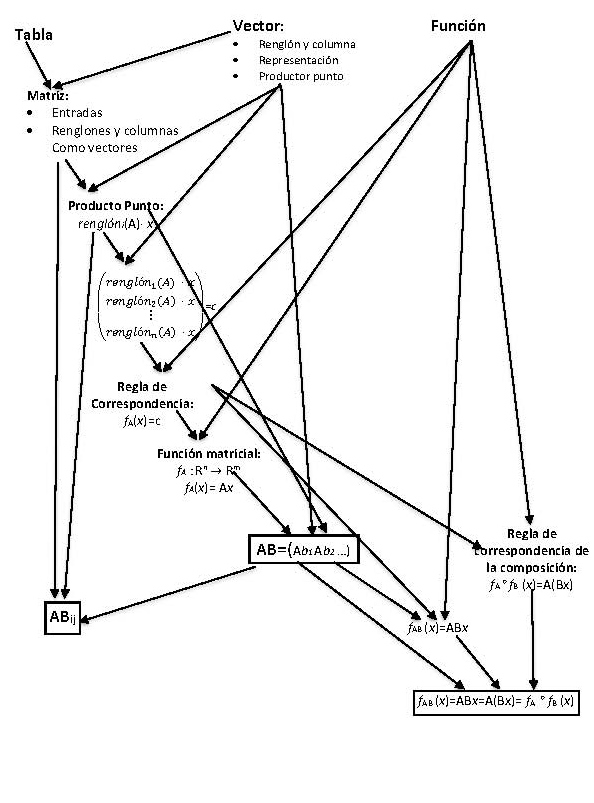
En la figura 1 mostramos el diagrama de una descomposición genética que aparece en el artículo [Pos+10] con el objetivo de ilustrar en la práctica cómo se diseña una de estas descomposiciones. No la explicaremos con detalle, pero la usaremos para ejemplificar algunas de las construcciones y mecanismos de la teoría APOE.
Esta descomposición genética busca describir una manera de encapsular la multiplicación de matrices y a su relación con la composición de funciones matriciales y fue el producto final de estudio de muchas otras. Lo primero que podemos observar es que en una descomposición se comienza por definir las construcciones básicas que deben de tener los estudiantes al comenzar a trabajar. Por ejemplo, en nuestro caso, notamos que los estudiantes no habían construido la matriz como proceso, que no habían interiorizado una matriz como una colección ordenada de vectores columna o renglón, lo que era fundamental para construir los conceptos objetivos del trabajo. Pensamos que también que habrían construido la función como proceso, pero tampoco fue así. A pesar de haber tomado varios cursos de cálculo, los alumnos no eran capaces de distinguir entre función y regla de correspondencia. Por lo que al inicio de la descomposición sólo aparecen la matriz como arreglo de valores con el vector y la función como proceso como pre-requisitos para iniciar las construcciones que deseamos que desarrollen.
Podemos notar que en la descomposición aparecen acciones, como la de calcular el producto punto de un vector con el renglón i-ésimo de una matriz dada, que al repetirse se interioriza como un proceso. En la figura se ve cómo este proceso se coordina con el proceso de vector para obtener el proceso de la multiplicación de una matriz con un vector.
Una observación importante es que a pesar de que los diagramas de una descomposición genética se describen de manera lineal, esto nos puede llevar a la conclusión errónea de que el aprendizaje es lineal. Esto es lejano a lo que se pretende con la teoría, distintos estudiantes pueden reflexionar de forma distinta y no lineal sobre las construcciones que se describen en la descomposición. Es decir una descomposición genética no refleja exactamente el aprendizaje de un individuo, ni es una regla sobre cómo el individuo debe construir los conceptos; lo que hace es proporcionar una herramienta que se puede evaluar y mejorar para diseñar procesos de instrucción más eficaces que permitan a un mayor número de alumnos en un grupo construir uno o varios conceptos matemáticos con un mayor nivel de profundidad.
La forma de implementar el marco teórico de APOE en la enseñanza es mediante el uso del ciclo de enseñanza ACE, que tiene tres componentes (A) actividades; (C) discusión en clase; (E) ejercicios.
Tomando en consideración cada una de las construcciones que se describen en una descomposición genética, apropiada para lo que se desea enseñar, se diseñan actividades que estimulen las construcciones y mecanismos propuestos. Estas actividades pueden ser muy diversas, en los orígenes de la teoría se realizaban utilizando programación por computadora. En el caso del ITAM, se ha promovido que las actividades tengan como origen una pregunta abierta de modelación matemática desde donde los estudiantes puedan ir aplicando sus conocimientos previos y construyendo nuevos conceptos. Por ejemplo, en el caso del trabajo sobre multiplicación de matrices el problema a modelar por los estudiantes era: “Tres tipos de pesticidas fueron rociados en cuatro tipos de plantas para eliminar insectos. Además en la región, cuatro tipos de herbívoros comen de las plantas. No sólo las plantas absorben estos pesticidas, también los herbívoros cuando comen las plantas. ¿Cómo podemos determinar la cantidad de cada pesticida que ha absorbido uno de los herbívoros?”
Las actividades se trabajan típicamente en equipos de manera colaborativa, pero la discusión en clase se puede introducir en cualquier momento. Ya sea porque exista una duda generalizada sobre las actividades, o para discutir o exponer la teoría del tema de las matemáticas que van surgiendo de las conclusiones de los estudiantes.
Como hemos dicho anteriormente, las actividades buscan promover las construcciones y mecanismos que modela la descomposición genética. Así, típicamente, cada una de las preguntas que se realizan tendrá un objetivo y una forma de entenderse mediante la teoría APOE.
Ejemplo: Los estudiantes trabajaron con una matriz A en la que la entrada $a_{ij}$ es la cantidad de miligramos de pesticida $i$ absorbidos por la planta $j$. Los estudiantes habían realizado las acciones de multiplicar a cada renglón de la matriz $A$ por un vector $\mathbf{x}$ y dieron su interpretación en términos del problema para llamar a $\mathbf{x}$ el vector de consumo de un pesticida.
Actividad: Encuentra la regla de correspondencia, dominio y codominio de una función que reciba al vector de consumo de un herbívoro y regrese el vector en el que cada entrada denote la cantidad de pesticida que absorbió dicho herbívoro.
En términos de APOE: Coordinación del proceso de multiplicación de matriz por vector con el proceso de función.
Las actividades se pueden dividir en una o varias sesiones. Al final de cada sesión se dota al alumno con problemas fuera del contexto del problema, pueden ser incluso ejercicios de libros de texto con el propósito de que practique y regrese a lo construido en clase y reconstruya, revierta y haga relaciones que lo ayuden a evocar el esquema que ha construido hasta ese momento.
Los resultados obtenidos en la investigación llevada a cabo con el ejemplo que hemos usado aquí, mostraron que la mayoría de los estudiantes de los grupos con los que se utilizó construyeron el producto de matrices como objeto y la transformación matricial como proceso, además de una relación clara entre ambos conceptos.
En este breve artículo hemos expuesto las nociones básicas del trabajo con la teoría de APOE. Hemos tomado como ejemplo la multiplicación de matrices, en donde el estudiante es capaz construir las definiciones necesarias relacionadas con el producto de matrices y la noción de composición de funciones sin que se comience con una definición impuesta, preestablecida y carente de interpretación para él. Aprender con APOE es mucho más cercano al trabajo que se realiza en la investigación en matemáticas, en donde se interpreta, se construye y donde es necesario tener la habilidad de resolución de problemas.
Existe una extensa bibliografía donde se plantean descomposiciones genéticas y actividades no sólo en el álgebra lineal, en cálculo o álgebra superior, por citar algunas áreas de las matemáticas que pueden servir como insumo para crear nuevas secuencias didácticas o evaluar las que generalmente usamos en el aula.
Por último, en las investigaciones se observa, que comenzar con un problema particular, con tintes de aplicación, brinda a los estudiantes con menor habilidad de abstracción la posibilidad de apoyarse en una idea concreta que promueve los mecanismos mentales para llegar a la encapsulación de los objetos y con ello a desarrollar de manera efectiva su capacidad de abstracción.
La investigación en educación matemática permite entender mejor el fenómeno del aprendizaje de las matemáticas. La investigación nos da pistas útiles para responder, aunque sea de manera parcial y provisional, la pregunta de cómo se aprenden las matemáticas. La teoría APOE en particular, nos proporciona una guía para diseñar actividades para que los alumnos aprendan más y mejor.