

El problema del einstein (del alemán ein uno stein piedra o pieza) se plantea la pregunta de si existe una tesela con la que cualquier teselación construida con copias de ella sea aperiódica. En la presente nota se expone el desarrollo histórico del problema, algunos intentos por resolverlo y un posible camino a seguir en busca de una solución definitiva.

Una teselación es un acomodo de piezas a las que llamaremos teselas que se pegan por sus bordes cubriendo todo el plano sin dejar agujeros. Las teselaciones han estado presentes para la humanidad desde hace más de dos mil años como patrones repetitivos decorativos en obras arquitectónicas. En los castillos de Alhambra, en Granada, España, construidos en el siglo xii, se puede encontrar no sólo una gran variedad mosaicos, sino indicios de un buen entendimiento del tema, ya que realizaron los diecisiete posibles tipos de simetría en diferentes mosaicos (figura 9). En la actualidad las teselaciones son utilizadas ampliamente en la vida cotidiana con fines decorativos o utilitarios como embaldosados, adoquinados, herrerías, etc. (figura 1), además de ser la herramienta usada para modelar los acomodos de los átomos en un sólido.
El primer estudio sobre teselaciones lo realizó Johannes Kepler en su libro de 1619 llamado Harmonices Mundi. En éste, Kepler trataba de explicar la armonía del universo y sus manifestaciones en términos geométricos, físicos y musicales.
Kepler decía que las figuras más armónicas y más perfectas eran los polígonos regulares. Cuando estas figuras se juntan se crea la congruencia, que Kepler define como:
Continúa Kepler:
Finalmente define la congruencia más perfecta como:
Kepler clasificó las congruencias más perfectas (figura 3) y las congruencias perfectas hasta con tres polígonos regulares y semirregulares (polígonos con todos sus lados iguales pero ángulos diferentes), analizando caso por caso (figura 4).
Kepler también podría ser considerado el fundador de la cristalografía, ciencia que estudia las formas de los cuerpos al cristalizar, es decir, el acomodo de los átomos en un sólido. Al matemático alemán le maravillaron las formas de los copos de nieve y dedicó el tratado De nive sexangula (El copo de nieve hexagonal) a su descripción. Ahí sugirió que los átomos de un sólido cristalino formaban empaques de esferas (figura 5). Los químicos adoptaron esta idea y desde entonces el estudio de acomodos de átomos en un cristal ha estado íntimamente relacionados con las teselaciones.
Sin embargo, para otros matemáticos, las ideas de Kepler pasaron aparentemente desapercibidas por casi tres siglos hasta que en 1891 Evgraf Fedorov, matemático, cristalógrafo y mineralista ruso, clasificó [9] las simetrías que pueden presentar los cristales en el espacio, es decir, las simetrías de teselaciones (cristalográficasUna teselación es cristalográfica si su subgrupo de traslaciones es del mismo rango que la dimensión del espacio donde vive la teselación. Esto se expondrá más adelante.) del espacio euclideano. Fedorov hizo un largo trabajo de enumeración de las 230 posibilidades, hoy llamadas grupos espaciales. Posteriormente clasificó también el caso más sencillo de las simetrías de cristales planos. Estos son conocidos como los diecisiete grupos cristalográficos o grupos mosaicos.
Pocos años después del trabajo de Fedorov, las teselaciones aparecieron en el problema 18 de la lista que David Hilbert postuló a comienzos del siglo pasado [14]. Constaba de tres incisos:

A finales del siglo pasado W. Thurston ideó una notación para tratar con las simetrías de superficies que J. Conway utilizó para obtener una clasificación de las simetrías de teselaciones mucho más elegante que la hecha por Fedorov.
Ésta consiste en asignar a cada tipo de simetría de la teselación un costo asociado con la característica de Euler, pensando en la teselación como un mapa encajado en el plano. Esto es, por mapa entendamos un dibujo con vértices, aristas y caras sobre una superficie; si a una teselación en el plano le aplicamos (la función inversa de) la proyección estereográfica, obtendremos un mapa en la esfera. Por lo que podemos definir la característica de Euler del plano igual a la de la esfera, que es 2.
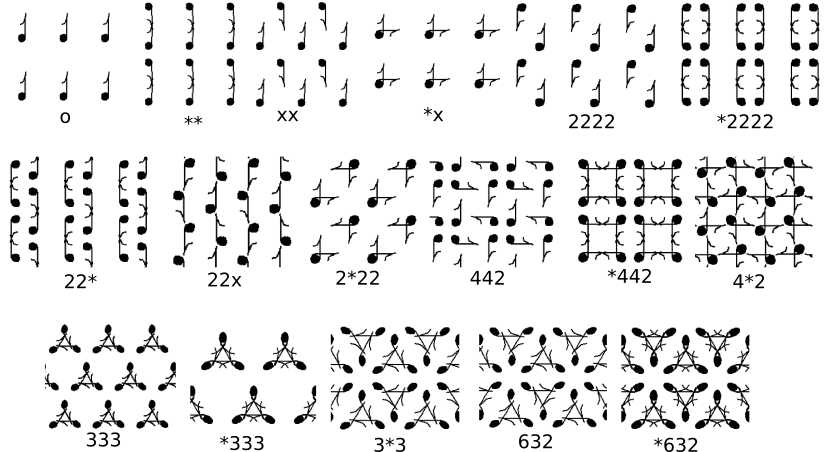
Toda la información necesaria la guarda un objeto geométrico llamado orbifold obtenido como el cociente de $\mathbb R^2$ por el grupo de simetrías $G$ de la teselación. Los orbifolds son espacios topológicos compactos, son localmente una variedad en todos sus puntos salvo en los puntos fijos bajo los elementos de $G$. Las singularidades y orientaciones de cada orbifold representan los tipos de simetrías de la teselación: puntos cono por cada centro de rotación simple, fronteras por reflexiones y torceduras por deslizamientos (figura 8).
La idea de la clasificación radica en el juego aritmético de conseguir sumar 2 (la característica de Euler del plano o esfera) a partir de los costos de las simetrías permitidas. Pero el objeto fundamental es el orbifold. Todos los detalles de este resultado se pueden encontrar en [7].

En la sección anterior platicamos sobre teselaciones periódicas sin decir qué significa eso de la periodicidad. Dicha exclusión se debe a la propia omisión del concepto durante el desarrollo histórico de las teselaciones.
Una teselación es periódica si es invariante bajo una traslación, es decir, si al recorrer la teselación por un cierto vector ésta permanece sin alteraciones. Todas las teselaciones que se expusieron en las secciones anteriores eran no sólo periódicas, sino cristalográficas, esto es, invariantes por traslaciones en tantas direcciones linealmente independientes como la dimensión de la propia teselación.
Existen diferentes definiciones de teselación aperiódica (figura 10). Nosotros las pensaremos como teselaciones que carecen de simetría traslacional, o sea que siempre que las recorras verás algo distinto, aunque pueden presentar otras simetrías como centros de rotación o ejes de reflexión. Casi todos los mosaicos de nuestro alrededor son realizaciones de teselaciones periódicas. En un mundo en el que la producción en serie estuviera menos arraigada quizás habría ejemplos de teselaciones aperiódicas por doquier. Al no ser así, para encontrar la aperiodicidad en nuestro entorno hay que remitirse de nuevo a la estructura interna de los sólidos, ya no cristalinos sino cuasicristalinos.
Los cuasicristales son sólidos que cumplen con todas las características de los cristales salvo que no caben dentro de la clasificación de Fedorov, pues presentan simetrías que se pensaban prohibidas para los cristales: pentagonal, octagonal, decagonal, dodecagonal. Fueron descubiertos por Dan Shechtman a principios de la década de los ochenta en aleaciones de aluminio y manganeso, pero la comunidad científica tuvo dificultades para aceptar y validar el hallazgo. No fue hasta 2011 que Shechtman fue galardonado con el Premio Nobel de química por su descubrimiento.

La aperiodicidad se había hecho manifiesta para los matemáticos un par de décadas antes, y fue traída a la luz por el matemático-lógico-filósofo chino-estadounidense Hao Wang en 1961. Él trabajaba en el problema del dominó, que consiste en preguntarse por la existencia de un algoritmo para decidir si un conjunto dado de dominós puede cubrir todo el plano o no. Los dominós, hoy conocidos como teselas de Wang (figura 11), son cuadrados del mismo tamaño con sus aristas coloreadas que se pueden pegar por sus aristas si los colores coinciden.
Wang demostró que dicho algoritmo existía siempre y cuando cualquier conjunto de dominós que admita una teselación admite también una teselación periódica [21]. Surgió entonces la pregunta, ¿cualquier conjunto de teselas de Wang que cubra el plano admite una teselación periódica, o existen conjuntos de teselas aperiódicos? Cabe decir que los conjuntos de teselas aperiódicos son aquellos que admiten únicamente teselaciones aperiódicas.
En 1967 Robert Berger, alumno de Wang, encontró un conjunto de más de 20 mil teselas de Wang que sólo admitía teselaciones no periódicas, con lo que demostró que el problema del dominó es indecidible [4].



A raíz de aquel primer conjunto aperiódico comenzaron a surgir rápidamente distintas variaciones. El mismo Berger encontró otros conjuntos aperiódicos más pequeños de teselas de Wang, al igual que Robinson quien halló uno de treinta y dos (las seis que aparecen en la figura 12 más algunas rotaciones y reflexiones de éstas). Posteriormente, en los setentas, Penrose y Ammann encontraron varios conjuntos aperiódicos de dos piezas con métodos distintos. Citando a Chaim Goodman-Strauss, “[...] se han descrito explícitamente alrededor de cuarenta conjuntos aperiódicos, la mayoría de ellos encontrados por arte misterioso” (cf. [11], donde también se encuentran referencias a dichas casi cuarenta descripciones).
Desde entonces ha estado presente la pregunta ¿existen conjuntos aperiódicos de una pieza? Este es el problema del einstein (del alemán ein uno stein piedra o pieza). Actualmente el problema puede considerarse resuelto o no, dependiendo de qué se entienda por tesela.
En 1997 Roger Penrose publicó un conjunto aperiódico de tres piezas conocido como el $(1+\varepsilon+\varepsilon^2)$, una de ellas de forma hexagonal con cuñas y muescas y las otras, que funcionan como vértices y aristas, pueden tomarse arbitrariamente pequeñas y delgadas (figura 14).
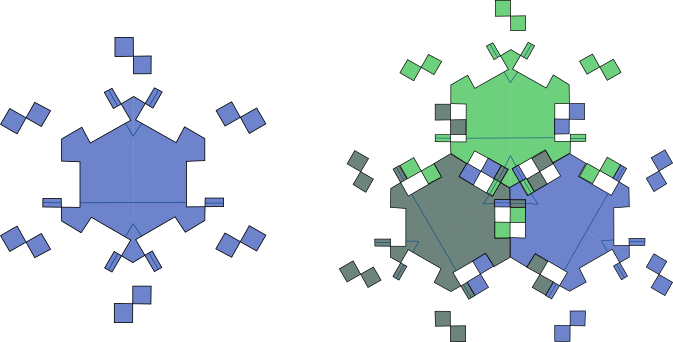
Siguiendo las ideas de Penrose, la matemática amateur Joan Taylor y posteriormente en colaboración con Joshua Socolar [20] de la universidad de Duke, obtuvo una pieza hexagonal que con coloraciones y reglas de pegado sobre los vecinos de los vecinos se obtienen sólo teselaciones aperiódicas. En un sentido estricto, cada una de las piezas coloreadas es un tipo diferente de tesela. La regla de pegado también se puede codificar en una tesela sin coloraciones pero disconexa (figura 15).
Otros intentos con diferentes variaciones han surgido por diversos agentes desde estudiantes de preparatoria hasta reconocidos matemáticos, incluyendo tesis doctorales dedicadas a la búsqueda de la monotesela [17], exploraciones con teselas de frontera fractal [8] o teselas con densidades [23].
No sabemos, pero aquí planteamos una idea de quien podría saber.
En el caso periódico sí hay teselaciones de cualquier tipo de simetría y con un único tipo de teselas. Esto se puede ver a través del orbifold asociado a cada teselación, ya que al ser una región fundamental del grupo de simetrías de la teselación, puede replicarse por simetrías para cubrir todo el plano. Por lo que el propio orbifold tiene toda la información para construir una monotesela periódica. Otra elección de monotesela periódica disponible para todos los grupos de simetría es la región fundamental de la retícula de traslaciones, que debe de ser uno de los polígonos de la figura 16.

Al darnos cuenta de que toda la información de la simetrías de una teselación periódica la guarda un objeto geométrico con unos cuantos datos combinatorios, uno quisiera saber quiénes son los orbifolds asociados a las teselaciones aperiódicas. Infelizmente no obtendremos orbifolds, pero igual se puede hacer el intento de obtener un objeto geométrico que acarree la información de las simetrías de una teselación aperiódica. Una posibilidad es el espacio de teselaciones, que se define a continuación.
Consideremos una teselación $T$ de $\mathbb R^2$ y $x\in\mathbb R^2$. La traslación de $T$ por el vector $x$ es la teselación
$$ T+x=\{t+x: t\in T\}, $$ la órbita de $T$ bajo esta acción es $$ \mathcal{O}(T)=\{T+x : x\in \mathbb R^2\}. $$ Equipamos a $\mathcal O(T)$ con una métrica en la que dos teselaciones $T,T'$ son $\varepsilon$-cercanas si existe $x$ en $\mathbb R^2$ de norma menor a $\varepsilon$ tal que $$ B_{\frac{1}{\varepsilon}}(0)\cap T+x = B_{\frac{1}{\varepsilon}}(0)\cap T'.$$Es decir, dos teselaciones son cercanas si coinciden en una bola euclideana de radio grande centrada en el origen salvo una pequeña traslación.
El espacio de teselaciones $\Omega_T$, también llamado la envolvente de la teselación $T$, se define como la completación de $\mathcal O(T)$ en esta métrica.
Notamos que si $T$ es cualquier teselación periódica entonces $\Omega_T$ es un toro, ya que las teselaciones se identifican por traslaciones. Para teselaciones aperiódicas, estos espacios son bastante más complicados. Han sido estudiados en la últimas décadas desde la topología y los sistemas dinámicos por Robert Williams, Lorenzo Sadun, Jean-Marc Gambaudo, Franz Gähler, Jared Anderson e Ian Putnam, entre otros. Los espacios $\Omega_T$ son una rica fuente de ejemplos en dinámica hiperbólica, son laminaciones por superficies de Riemann [10], límites inversos de variedades ramificadas [2, 18, 3] y haces fibrados sobre toros con fibras homeomorfas al conjunto de Cantor [22, 19].
Sin embargo, para hacer la analogía explícita entre los orbifolds asociados a teselaciones periódicas y los espacios de teselaciones aperiódicas es necesario cruzar un pantano, pues las “simetrías” de teselaciones aperiódicas “densifican” el espacio $\Omega_T$ de manera que el cociente bajo “simetrías” carece de topología. Algo muy similar a lo que sucede con el espacio de hojas de la foliación del toro por rectas de pendiente irracional. A raíz de esto han surgido estudios de espacios de teselaciones desde enfoques geométricos generalizados, como geometría no-conmutativa [6, 2]. Otra opción es dotar a los espacios de teselaciones con una estructura de difeología.
La difeología es una generalización de estructura geométrica desarrollada en las últimas dos o tres décadas. Ésta nació en Francia impulsada por Jean-Marie Souriau y sus estudiantes Paul Donato y Patrick Iglesias. Este último es el autor de la mejor referencia disponible hasta el momento [15], que fue apenas publicada en 2013, aunque desde hace varios años ya circulaba por la red un borrador bastante completo.
El fundamento de la difeología es hacer geometría diferencial sin coordenadasYo lo interpreto como lo que ocurre al pasar de espacios métricos a topológicos.. Los espacios difeológicos son una clase de espacios que generalizan la definición de variedad “olvidando” la topología pero manteniendo su estructura suave. La idea de utilizar esta herramienta para el estudio de espacios de teselaciones se concentra en el ejemplo del toro irracional $T_\alpha = \mathbb R/ (\mathbb Z + \alpha \mathbb Z$). Este ejemplo es uno de los pilares de la teoría difeológica por adquirir una estructura que la topología no alcanza a distinguir.
Dotando a $\Omega$ de una difeología, el haz fibrado sobre el toro definido por Williams se puede definir más naturalmente sobre el toro irracional $T_\alpha$ (en el caso unidimensional [1]). La mayor naturalidad radica en que la construcción de Williams consiste en deformar las teselas para que todos los vértices tengan coordenadas enteras. Esto se puede hacer sin modificar la combinatoria de la teselación pero dará como resultado una equivalencia muy débil entre espacios de teselaciones (homeomorfismo, más débil que conjugación, más débil que derivabilidad local mutua). La posibilidad de definir una estructura geométrica sobre $T_\alpha$ permite construir una versión de aquel haz pero conservando información importante como los tamaños de las teselas. Dicho haz, en el caso periódico, recupera los orbifolds. En este sentido, quien podría guardar la respuesta sobre la existencia de la monotesela aperiódica es el espacio de teselaciones $\Omega_T$, pues el problema de la monotesela suena y resuena a un problema de encajabilidad de $\Omega_T$ en superficies.