

En su primera visita a la Ciudad México (en la vida), Shigefumi Mori dio una charla en la unam. El resumen de ésta comenzaba:
En dicha plática de diciembre del año 2017, el profesor Mori se abocó a explicar un trabajo merecedor de la Medalla Fields (la que él ganó en el año 1990) sobre la clasificación birracional de variedades algebraicas. Veintiocho años después la Organización Internacional de Matemáticos (ium, por sus siglás en inglés), y siendo Mori su presidente, le otorga la Medalla Fields a Caucher Birkar por sus contribuciones a la geometría birracional. Estas medallas se han atribuido a una línea de investigación bien definida dentro de la geometría algebraica, y uno de los propósitos de este artículo es esbozarla.
La historia de este escrito comenzará con el trabajo de Guido Castelnuovo y Federigo Enriques en Roma, Italia en el año 1901, y terminará comentando las contribuciones de Caucher Birkar. Dado que estos autores están separados por casi ciento veinte años, hilvanaremos las ideas de este texto con cuatro artículos principales: [2, 3, 11, 12]; elegimos sólo estos con la intención de dar cohesión al presente escrito.
El lector advertirá que sólo una de dichas referencias estudia objetos de dimensión $2$, mientras que el resto se concentra en objetos de dimensiones altas, lo que implícitamente sugiere los prerrequisitos de este texto y señala el área de la geometría en la que nos enfocaremos. Adicionalmente a las fuentes escritas, nos auxiliaremos de la charla del profesor Mori en México [10] para darle coherencia a la historia de este artículo.
El conjunto de todas las variedades algebraicas es basto. De ahí que intentemos organizarlas en clases de equivalencia. El conjunto de clases puede ser complicado, y saber qué variedades pertenecen a la misma clase puede ser un reto importante. La geometría birracional y en particular el programa del modelo minimal desean hallar un representante “sencillo” en cada clase de equivalencia birracional (para después clasificarlos; por ejemplo estudiar su espacio moduli). La equivalencia birracional será un concepto central de este escrito y su definición se incluye en el recuadro 1. Además, es una noción un tanto única de la geometría algebraica; en topología o geometría diferencial no existen nociones análogas estríctamente hablando.
En dimensión $1$, un representante sencillo de una clase de equivalencia birracional es simplemente una curva suave. En dimensión $2$, un representante sencillo es una superficie sin curvas rígidas. En dimensiones más altas hallar uno de estos representantes es un reto importante y la investigación que relatamos aquí se encamina a demostrar que en efecto se puede hacer. Ver recuadro 6.
En lo que sigue, nos abocaremos a describir detalles del párrafo anterior tratando casos separados según su dificultad. El lector advertirá, en un momento condescendiente, que este escrito es una caricatura del desarrollo y tecnicismo de la obra que deseamos esbozar y no tanto detallar.
El profesor Mori resumió la clasificación birracional de las curvas (variedades algebraicas de dimensión $1$) en una diapositiva de su ponencia [10]. En ella incluyó el trabajo de Bernhard Riemann, el de Felix Klein y el de una decena de matemáticos; concluyó que: toda curva algebraica $B$ es birracional a una curva suave de género $g$ menos un número finito de puntos. En otras palabras, si agrupamos a las curvas algebraicas en clases de equivalencia birracional, entonces en cada clase existe una curva suave.
Una equivalencia birracional entre curvas suaves proyectivas extiende a un isomorfismo. La topología de este tipo de curvas está determinada por un número natural — el género— y fijando éste, nos podemos preguntar por el conjunto de clases de equivalencia birracional ($i.e.$, isomorfismo) de curvas suaves de género $g$. ¡Este conjunto es una variedad algebraica!, se llama espacio moduli de curvas y se denota $M_g$.
Para géneros pequeños, como $g=1,2,3$, la variedad $M_g$ se entiende relativamente bien. En general, muchos aspectos de su geometría (birracional) son aún misteriosos. Un caso muy especial es el de curvas racionales, $g=0$; topológicamente equivalentes a la esfera $S^2$. La variedad $M_0$ consiste de un punto.
Sin perder generalidad, podemos concentrarnos en una superficie suave $S$ e investigar su clase de equivalencia birracional. Por ejemplo, ¿existe en esta clase una superficie $S'$ más sencilla que $S$? Mori en su charla indica: “un problema central es cómo encontrar un modelo minimal para una superficie suave $S$”. La palabra “sencilla” quiere decir eliminar las curvas excepcionales o rígidas; ver el recuadro 1 para un ejemplo y el recuadro 2 para la definición.
Una cónica en el plano $\PP^2$, tiene como ecuación $$ax^2+bxy+cxz+dy^2+eyz+fz^2=0.$$ Consideremos todas las cónicas que pasan por el punto $p=[1:0:0]\in \mathbb{P}^2$. Éstas se describen con la ecuación $$bxy+cxz+dy^2+eyz+fz^2=0,$$ y por tanto podemos dotar a este conjunto de estructura y coordenadas: $[b:c:d:e:f]$, que identificamos con coordenadas del espacio proyectivo $\PP^4$. Con esta información, obtenemos una aplicación racional $$\sigma:\PP^2\dashedrightarrow \PP^{4*}$$ definida como $[x_0:y_0:z_0]\mapsto [x_0y_0:x_0z_0:y_0^2:y_0z_0:z_0^2]$. Observemos, $\sigma$ está bien definida en el abierto $\PP^2\backslash \{p\}$. Más aún, este abierto de $\PP^2$ es isomorfo a la imagen de $\sigma$, y dicha imagen yace en la superficie de $\PP^{4*}$ definida por las ecuaciones $$W^2-ZT=XT-YW=XW-YZ=0.$$
Esta superficie, denotada $\mathrm{Bl}_p\PP^2$, contiene una línea $E$ definida por las ecuaciones $Z=W=T=0$. Esta línea es el complemento de la imagen de $\sigma$. Por lo tanto $\PP^2\backslash \{p\}$ es isomorfo a $\mathrm{Bl}_p\PP^2\backslash \{E\}$ y tenemos que $\PP^2$ y $\mathrm{Bl}_p\PP^2$ son birracionales. ■
Las ecuaciones de $\mathrm{Bl}_p\PP^2\subset \PP^{4*}$ nos indican que es una superficie reglada. Es decir, contiene una familia de líneas, llamadas reglas, que las denotamos como $L_{[a:b]}$, y cuyas ecuaciones son $$aW-bT=aZ-bW=aX-bY=0,$$ donde $[a:b]\in\PP^1_{a,b}$. Las reglas $L_{[a:b]}$ y $E$ son todas las líneas contenidas en $\mathrm{Bl}_p\PP^2$.
Las ecuaciones revelan que cada punto de $\mathrm{Bl}_p\PP^2$ está contenido en una regla y que la intersección $|L_{[a:b]}\cap L_{[c:d]}|=0$, si $[a:b]\ne [c:d]$. En contraste, la línea $E$ es excepcional y no se mueve; es rígida. La primera afirmación nos dice que existe un morfismo $\mathrm{Bl}_p\PP^2\rightarrow \PP^1_{a,b}$. Lo segundo, que la autointersección $E^2=-1$.
Justifiquemos ingenuamente la notación $E^2=-1$. Si $L,L'\subset \PP^2$ son dos líneas, la imagen $\sigma(L)$ es una cónica suave en $\PP^4$ si $p\notin L$. Sin embargo, si $L,L'$ contienen el punto $p=[1:0:0]$, entonces la imagen $\sigma(L)$ es una componente de la cónica singular $E \cup L_{[a:b]}$. Dado que $|L_{[a:b]}\cap E|=1$, entonces tenemos que $1=|L\cap L'|=|(E\cup L_{[a:b]})\cap (E\cup L_{[c:d]})|$, de donde formalmente deducimos que $|E\cap E|=E^2=-1$.
Observemos que la aplicación inversa $\sigma^{-1}$ se puede definir sobre toda la superficie $\mathrm{Bl}_p\PP^2$, simplemente mandando $E$ al punto $p$. Esto es, $\sigma^{-1}:\mathrm{Bl}_p\PP^2\rightarrow \PP^2$ es un morfismo que contrae la línea excepcional $E$.
El paso crucial para hallar el modelo minimal de una superficie que no sea reglada aparece en el artículo questioni [3] de Castelnuovo y Enriques. Éste consiste en eliminar las curvas excepcionales: “la possibilità di eliminare le curve eccezionali per ogni superficie che non appartenga alla famiglia delle rigate”. Con este resultado, procedemos a encontrar el modelo minimal de una superficie como sigue: empezamos con una superficie suave $S$. Si $C\subset S$ es una curva excepcional, entonces se contrae a un punto de una superficie $S'$. Si $S'$ contiene una curva excepcional, entonces repetimos una contracción. De lo contrario, $S'$ es el modelo minimal de $S$.
En cada contracción del proceso anterior, remplazamos una esfera $S^2$ por un punto. Por lo tanto, el segundo número de Betti $b_2(S)$, decrece. Como dicho número es positivo para toda superficie proyectiva, entonces el proceso anterior termina en a lo más tantos pasos como $b_2(S)$. Concluimos que es posible encontrar una superficie $S_{\tiny{min}}$ sin curvas excepcionales $$S\rightarrow S'\rightarrow \cdots \rightarrow S_{\tiny{min}}.$$
El proceso de eliminar una curva excepcional está ejemplificado en el recuadro 1. Ahí, el morfismo $\sigma^{-1}:\mathrm{Bl}_p\PP^2\rightarrow \PP^2$ contrae la línea $E$ ($\cong \PP^1$). En la figura 2, cortesía de Alex Massarenti, se caricaturiza la explosión $\mathrm{Bl}_p\PP^2$, y la línea $E$ es etiquetada como $\xi \times \PP^1$.
El interés de Castelnuovo y Enriques en el questioni no es únicamente demostrar que las curvas excepcionales se pueden contraer. Los autores buscan también clasificar superficies minimales además de probar que el modelo minimal de una superficie que no sea reglada se encuentra contrayendo un número finito de curvas excepcionales (en la forma equivalente de “no existencia de curvas de $2^{\tiny{do}}$ tipo” [3].) En ese artículo también se caracteriza a las superficies regladas: “tutte le superficie sopra cui il procedimento di aggiunzione si estingue... le superficie dotate di questa propieta sono riferibili a rigate”. Esta propiedad persistirá en dimensiones altas, comparar recuadros 2 y 6.
Una curva excepcional $E$ es isomorfa a $\PP^1$ y además es rígida. El siguiente resultado caracteriza numéricamente estas curvas y justifica su nombre.
El questioni [3] caracteriza las superficies regladas y en él además se establece la unicidad del modelo minimal que ahora enunciamos.
El estudio de las superficies algebraicas es una de las herencias vigentes de la escuela italiana de geometría algebraica de principios del siglo XX; donde algunos apellidos insignia son Castelnuovo, Enriques, Severi, Fano, Segre (Beniamino y Conrado). Dicho estudio culminó con la clasificación de Kodaira-Enriques. Una referencia con notas históricas es [5]. Para una exposición más técnica ver [1].
Shigefumi Mori comenzó a escribir instrucciones para hallar el modelo minimal de un sólido en el artículo fundamental canonical [11] del año 1982. Éstas, como en el caso de superficies, tratarán de contraer curvas racionales ($\cong \PP^1$), las cuales serán de dos naturalezas: rígidas o reglas de una superficie. El siguiente párrafo demanda mucho del lector pues enunciaremos ideas sin preámbulo y abordaremos los detalles después.
Las ideas del canonical que marcaron un parteaguas en la geometría birracional son tres. Comencemos con un sólido suave $X$. Primero, si el divisor canónico $K_X$ es negativo sobre alguna curva $C\subset X$ ($i.e.$, $K_X.C\menorque0$), entonces existe una curva racional (candidata a ser contraída). Segundo, de entre todas estas curvas, Mori identifica las extremadamente negativas: éstas inducen los llamados rayos extremales; ingrediente central del teorema del cono de curvas. Tercero, Mori muestra que dichas curvas extremales pueden contraerse y describe los resultados de estas contracciones. El recuadro 3 incluye definiciones, notación y ejemplos.
Si $\mathrm{dim }\ \!M \ge 2$, el divisor canónico $K_M$ formalmente se puede intersecar con una curva $C$, y obtener un número racional. La notación es $K_M.C$.
La primera contracción produce el modelo minimal de $S$. La segunda una fibración.
Del párrafo anterior se pueden escribir instrucciones para hallar el modelo minimal de un sólido $X$: si $K_X$ es negativo en alguna curva, identificar la que induzca un rayo extremal y contraerla. Esto nos dará un morfismo $\phi:X\rightarrow Y$. Si $K_{Y}$ es negativo en alguna curva, repetimos el proceso en $Y$. En un número finito de pasos $$X\overset{\phi}{\rightarrow} Y\rightarrow \cdots \rightarrow X_{\tiny{min}},$$ hallamos una variedad $X_{\tiny{min}}$, tal que el divisor canónico $K_{X_{\tiny{min}}}$ no interseca a ninguna curva negativamente (i.e., $K_{X_{\tiny{min}}}.C\ge 0$ para toda curva). Estas instrucciones son llamadas “programa del modelo minimal” o mmp por sus siglas en inglés.
Programa del modelo minimal para superficies según el canonical [11]:
El programa de arriba tiene, al menos, dos obstáculos que necesitan comentarse. El primero, la contracción de una curva racional extremal podría producir una singularidad en el sólido $Y$. Por lo tanto, hay que llevar a cabo el programa con sólidos no necesariamente suaves. Este programa se escribió en [13] por Miles Reid.
Las singularidades que se introducen nos llevan a otro obstáculo del programa de Mori: al contraer una curva extremal, el sólido resultante $Y$ podría ser tan singular que las curvas extremales no pueden determinarse, y el programa no sabe cómo continuar. Estas curvas anómalas existen y a menudo son curvas rígidas (ver recuadro 1).
Citaremos un segundo artículo de Mori del año 1988, el célebre existence [12]. En él, se explica cómo superar el obstáculo de arriba: en lugar de contraer una curva anómala, construimos otra variedad $X'$, cuya virtud es satisfacer un diagrama de intercambio; flip en inglés. La existencia de esta variedad $X'$ se establece en [12]. Dicha $X'$ resulta ser manejable y entonces ahí continuamos con el programa. Resulta que este paso completa el conocido programa de Mori. Será mejor exhibir dicho programa con un dibujo original del existence. Inmediatamente después explicaremos su nomenclatura.
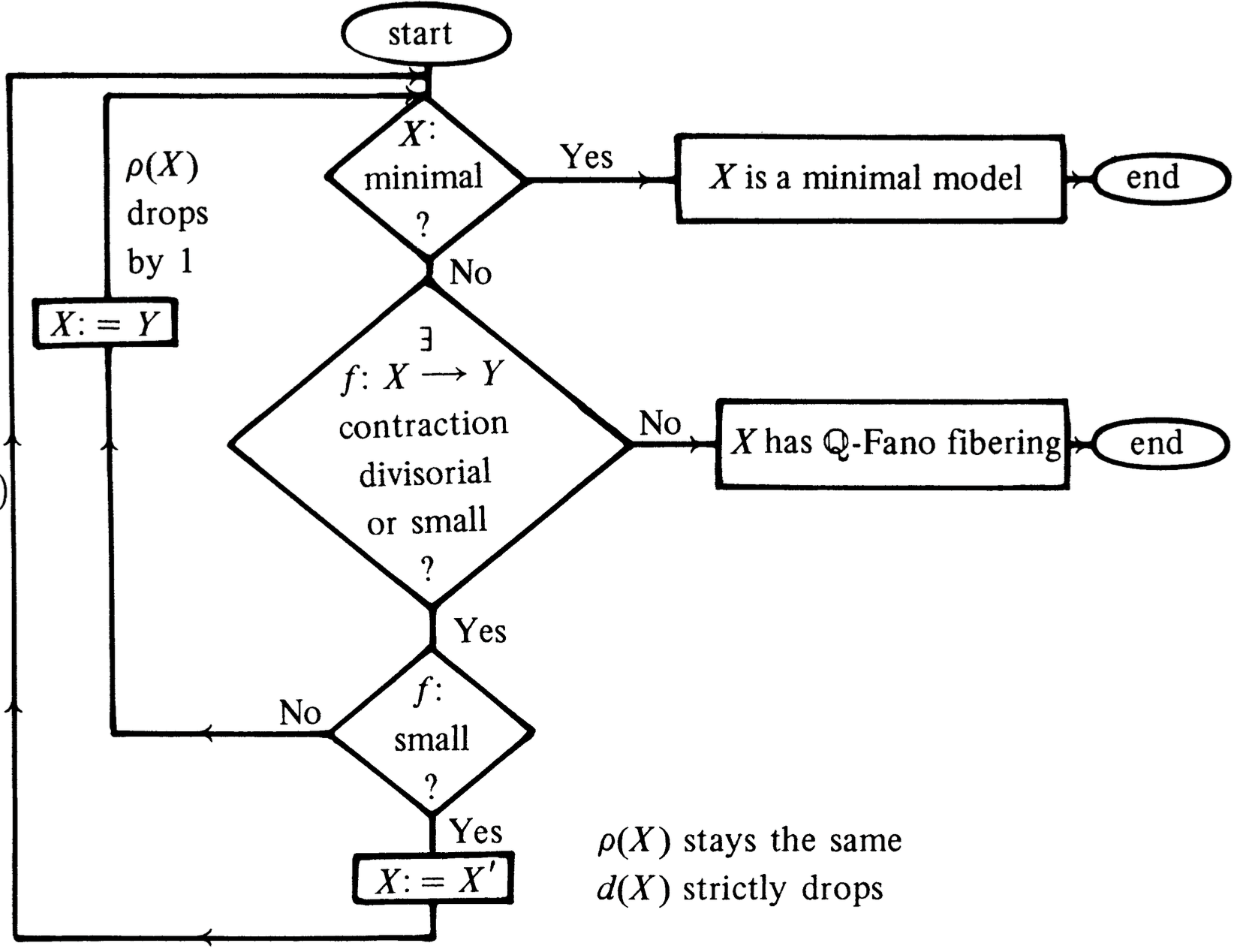
En la figura $3$, contraction divisorial corresponde a contraer subvariedades de codimensión $1$. Éste es el caso de una explosión y cuando las curvas que se contraen son reglas de una superficie. Por otro lado, la small contraction corresponde a contraer una curva anómala, es decir, rígida. En este caso se intercambia a $X$ por $X'$ (flip), y se continúa el programa en $X'$. El número $\rho(X)$ es a menudo el segundo número de Betti, y el número $d(X)$ es llamado dificultad y fue introducido por Vyacheslav Shokurov [14].
Por otro lado, una consecuencia central del existence [12], usando que los intercambios existen en dimensión $3$, es que el mmp se puede compilar. Lo enunciamos a continuación.
Caucher Birkar, Alessio Corti, Christopher Hacon y James Mckernan demuestran en otro célebre artículo del año 2009, el bchm [2], que el modelo minimal de una variedad $X$ se puede hallar si el divisor canónico $K_X$ es una subvariedad; y no sólo una suma formal de subvariedades.
Si observamos el programa de Mori en dimensión tres, éste no especifica qué curva extremal empezar a contraer entre las posibles opciones. El programa del modelo minimal con escalares limita las opciones para empezar a contraer y demuestra que el modelo minimal se puede hallar. Ver el recuadro 6.
Un obstáculo serio en el programa sin escalares es saber si los intercambios de una contracción anómala terminan o no. Es decir, en este caso no se conoce un número como la dificultad de Shokurov; ver los recuadros 5 y 7. Sin embargo, la existencia de intercambios, generalizando el existence [12], es consecuencia del bchm [2].
Resumiendo, las instrucciones del modelo minimal en general sugieren que empecemos con una variedad $X$ no muy singular, si $K_X$ es nef, entonces $X$ es minimal. Si $K_X$ no es nef, entonces existe otra variedad $X_{\tiny{min}}$, y una aplicación $$X\overset{\phi}{\rightarrow} X_{\tiny{min}},$$ tal que el divisor canónico $K_{X_{\tiny{min}}}$ es nef, y por tanto esta variedad es minimal. Más aún, nos indicaría que $\phi$ es una composición de contracciones divisoriales (explosiones) e intercambios de curvas anómalas. Una utilidad de esto sería conocer los mecanismos para construir todas las variedades algebraicas a partir de las minimales. Recuadro 7.
Esta conjetura es cierta para $n\le 4$ [8], pero en general es un problema abierto e implicaría lo siguiente:
La junta general de la Organización Internacional de Matemáticos (ium, por sus siglas en inglés) se reunió previo al Congreso Internacional de Matemáticos de Río de Janeiro para votar asuntos variados. Entre dichos asuntos acordaron que nadie sería premiado por la ium más de una ocasión.
Días después, Caucher Birkar recibía públicamente la Medalla Fields por segunda ocasión. Esto a raíz de un hecho desafortunado (le robaron la medalla minutos después de entregada —por primera ocasión— estando en la ceremonia de premiación entre el tumulto, las fotos y las entrevistas). El hurto generó aún más entrevistas en donde la prensa internacional reportó —de manera quizá involuntaria— la importancia de las variedades $\mathbb{Q}$-factoriales y del programa del modelo minimal; hecho afortunado para acercar la geometría birracional (y sus logros) a una audiencia amplia.
El presente artículo se financió con el programa Cátedras conacyt, 2014-I y con el proyecto conacyt de ciencias básicas cb-2015/253061. Agradezco la generosidad de Elisa T Hernández, Rita Jiménez, Manuel Leal y Monserrat Vite pues su lectura cuidadosa contribuyó a mejorar sustancialmente la exposición de este escrito.