

En esta nota veremos, mediante una serie de ejemplos, el problema de encontrar modelos compactos de geometrías homogéneas: resultados de existencia, no existencia y problemas abiertos. Daremos, mediante estos ejemplos, un paseo fugaz por la geometría, aritmética, topología y dinámica que aparecen en este problema.
Siguiendo la filosofía del programa Erlangen de Felix Klein (1849-1925) [Kle08], podemos entender una geometría mediante el grupo de transformaciones que la dejan invariante, por lo que es interesante estudiar las geometrías que son más simétricas. Una manera de hacerlo es considerando las geometrías homogéneas, que son aquellas para las que cualesquiera dos puntos son indistinguibles. Así, una geometría homogénea está dada por un espacio modelo $X$ y un grupo de simetrías $G = Iso(X)$ de manera que cualesquiera dos puntos de $X$ están conectados por un elemento de $G$. Más aún, podemos pensar en espacios $\widehat{X}$ modelados en $X$, es decir tal que $\widehat{X}$ se ve localmente como $X$ y podemos preguntarnos ¿qué tan compatible es la geometría de $X$ con la existencia de un modelo compacto $\widehat{X}$?
Vamos a adentrarnos en este problema, pero antes, comencemos haciendo más explícita la pregunta. Si el grupo de simetrías $G = Iso(X)$ también tiene estructura diferenciable, es decir, es un grupo de Lie, entonces se tiene naturalmente una identificación $X = G/H$, con $H$ algún subgrupo cerrado y una manera de obtener una variedad localmente modelada en $X$ es tomar un subgrupo discreto $\Gamma \subset G$ de manera que el cociente $\pi : G/H \rightarrow \widehat{X} = X / \Gamma$ sea un cubriente, pero ¿existirá $\Gamma$ de manera que $X/\Gamma$ es compacto?
Una situación en la que $G$ es grupo de Lie ocurre cuando $X$ es una variedad riemanniana [ONe83], [Kob95], es decir, la geometría está dada infinitesimalmente por un producto interno positivo definido \begin{equation*} \mathcal{G}_x : T_x X \times T_x X \rightarrow \R, \end{equation*} en cada punto $x \in X$ y podemos analizar qué pasa en dimensiones pequeñas.
En dimensión $2$ ser homogéneo es equivalente a tener curvatura constante $k$ [Rat06] y podemos distinguir tres casos:
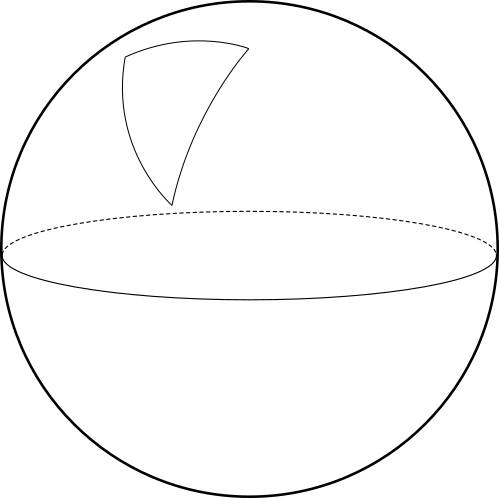
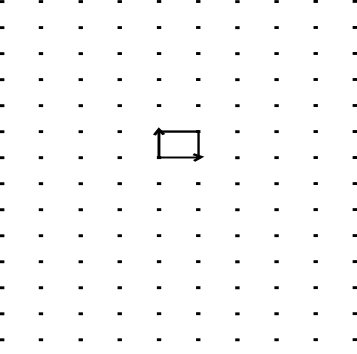
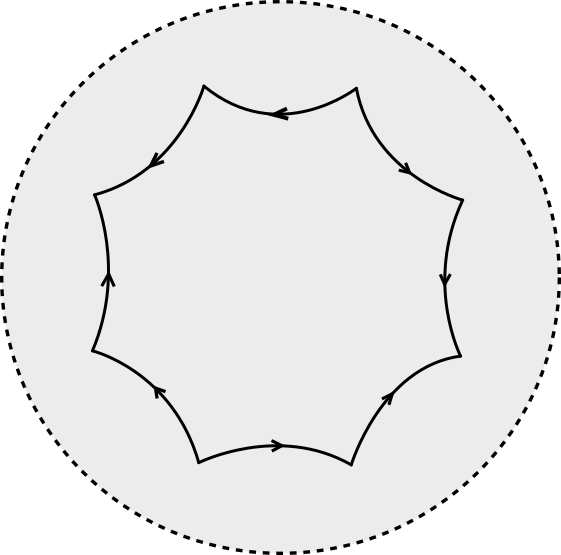
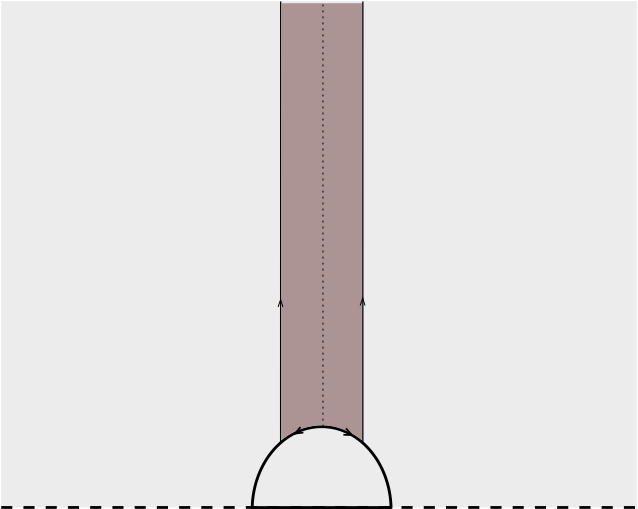
En el caso de curvatura positiva, el espacio modelo es compacto, en los otros dos casos podemos tomar un polígono con lados geodésicos como muestra la figura 1 y al pegar estos lados (la figura 2 muestra el proceso de pegado para el caso de curvatura negativa), obtenemos modelos compactos de curvatura constante, figura 3.
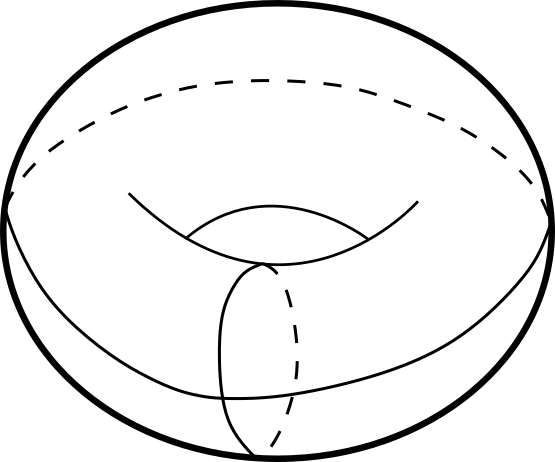
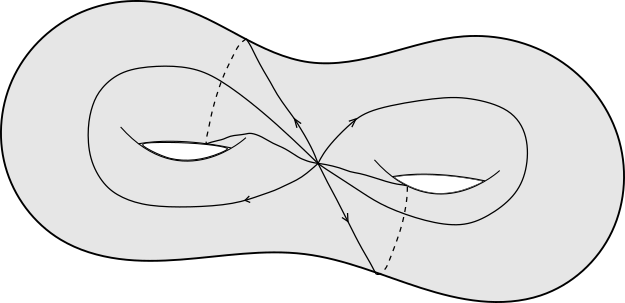
En dimensión $n \mayorque 2$, podemos construir de manera análoga los modelos de curvatura constante $S^n$, $\R^n$ y $\mathbb{D}^n$, sin embargo, ser homogéneo ya no es equivalente a tener curvatura constante, pues tangente a un punto podemos tener pares de direcciones de distintos tipos y por tanto distintas curvaturas. En dimensión $3$, de acuerdo con el trabajo de William Thurston (1946-2012), tenemos sólo otras 5 posibilidades para geometrías homogéneas además de las de curvatura constante ([Thu97], [Sco83]):
\begin{equation*} \mathbb{D}^2 \times \R, \ S^2 \times \R, \ Nil, \ Sol, \ \widetilde{SL_2}. \end{equation*}
Así, entre los ejemplos de modelos compactos para geometrías homogéneas tendremos
\begin{equation*} S^3, \ S^2 \times \R / \Z, \ \R^3 / \Z^3, \ \Sigma \times \R / \Z, \end{equation*}
donde $\Sigma$ es una superficie de curvatura negativa. La geometría Nil se obtiene considerando el grupo de matrices triangulares superiores
\begin{equation*} H = \left\{ \left(\begin{array}{ccc} 1 & x & z \\ 0 & 1 & y \\ 0 & 0 & 1 \end{array}\right) : x,y,z \in \R \right\}, \end{equation*}
conocido como grupo de Heisenberg que como variedad es equivalente a $\R^3$, pero como grupo es más interesante pues su centro
\begin{equation*} N = \left\{ \left(\begin{array}{ccc} 1 & 0 & z \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right) : z \in \R \right\} \end{equation*}
es tal que $N \cong \R$ y $H / N \cong \R^2$, pero la sucesión exacta
\begin{equation*} 1 \rightarrow N \rightarrow H \rightarrow \R^2 \rightarrow 1 \end{equation*}
no se escinde, es decir, $H$ y $\R \times \R^2$ no son isomorfos como grupos. Imponiendo la condición de tener la métrica euclidiana $dx^2 + dy^2 + dz^2$ en el espacio tangente a la identidad $I \in H$ que corresponde al punto $(0,0,0) \in \R^3$ y de manera que las traslaciones
\begin{equation*} L_g : H \rightarrow H, \qquad L_g(h) = gh \end{equation*}
sean isometrías para todo $g \in H$, entonces la métrica en un punto arbitrario $(x,y,z) \in \R^3$ está dada por $ds^2 = dx^2 + dy^2 + (dz - xdy)^2$. Si procedemos como sugiere la observación 1, tomando el subgrupo discreto
\begin{equation*} \Lambda = \left\{ \left(\begin{array}{ccc} 1 & x & z \\ 0 & 1 & y \\ 0 & 0 & 1 \end{array}\right) : x,y,z \in \Z \right\}, \end{equation*}
tendremos una fibración
\begin{equation*} \R / \Z \rightarrow H / \Lambda \rightarrow \R^2 / \Z^2, \end{equation*}
de manera que $H / \Lambda$ es compacto. La geometría Sol se puede obtener de manera parecida a Nil y construir un modelo compacto $S$, donde ahora tendremos una fibración
\begin{equation*} \R^2 / \Z^2 \rightarrow S \rightarrow \R / \Z. \end{equation*}
De hecho, se pueden construir modelos compactos para todas las geometrías de Thurston tomando retículas de puntos enteros
en el grupo de simetrías, pero esta construcción es más delicada en las dos geometrías que faltan por describir. Esto lo haremos en la sección siguiente, pero por el momento vemos por qué es delicado el proceso ejemplificándolo en el caso de la geometría $SL_2$. Consideramos el semiplano superior
\begin{equation*} \mathbb{H}^2 = \{ x + iy : x,y \in \R, \ y \mayorque 0 \} \subset \C \end{equation*}
con la geometría dada por la métrica $ds^2 = (dx^2 + dy^2)/y^2$, que es otro modelo de geometría de curvatura constante $-1$ y el grupo matricial
\begin{equation*} SL_2(\R) = \left\{ \left(\begin{array}{cc} a & b \\ c & d \end{array}\right) \in GL_2(\R): ad - bc = 1 \right\}, \end{equation*}
actuando por isometrías en $\mathbb{H}^2$ por transformaciones de Moebius
\begin{equation*} \left(\begin{array}{cc} a & b \\ c & d \end{array}\right) \cdot z = \frac{a z + b}{ c z + d}. \end{equation*}
La identificación de los dominios complejos $\mathbb{D}^2 \cong \mathbb{H}^2$ nos da el isomorfismo de grupos $SU(1,1) \cong SL_2(\R)$, más aun, si identificamos el subgrupo de isotropía en el elemento imaginario
\begin{equation*} SO(2) = \left\{ \left(\begin{array}{cc} a & b \\ -b & a \end{array}\right) \in GL_2(\R): a^2 + b^2 = 1 \right\}
= \{A \in SL_2(\R) : A \cdot i = i \}, \end{equation*}
tenemos una fibración
\begin{equation*} SO(2) \rightarrow SL_2(\R) \rightarrow SL_2(\R)/SO(2) \cong \mathbb{H}^2. \end{equation*}
Topológicamente tenemos la identificación $SL_2(\R) \cong S^1 \times \mathbb{H}^2$ (pero esta identificación no es isométrica), así un modelo para la geometría $SL_2$ es el cubriente universal $\widetilde{SL_2(\R)}$, topológicamente $\mathbb{R}^3$, con una métrica invariante por multiplicaciones izquierdas. Si tomamos ahora el grupo de puntos enteros
\begin{equation*} SL_2(\Z) = \left\{ \left(\begin{array}{cc} a & b \\ c & d \end{array}\right) \in SL_2(\R): a, b, c, d \in \Z \right\}, \end{equation*}
tendremos una fibración
\begin{equation*} S^1 \rightarrow SL_2(\Z) \backslash SL_2(\R) \rightarrow SL_2(\Z) \backslash \mathbb{H}^2, \end{equation*}
sin embargo, el espacio $SL_2(\Z) \backslash SL_2(\R)$ no es compacto, aunque sí tiene volumen finito, pues tenemos que
\begin{equation*} SL_2(\Z) \backslash \mathbb{H}^2 = D /\thicksim , \qquad D = \{ x + i y \in \mathbb{H}^2 : x^2 + y^2 \geq 1, \ |x| \leq 1\}, \end{equation*}
con las relaciones $\{ \eta \thicksim - \overline{\eta} : Re(\eta) = 1/2 \textrm{ o } |\eta| = 1\}$ y este espacio no es compacto, como muestra la figura 4.
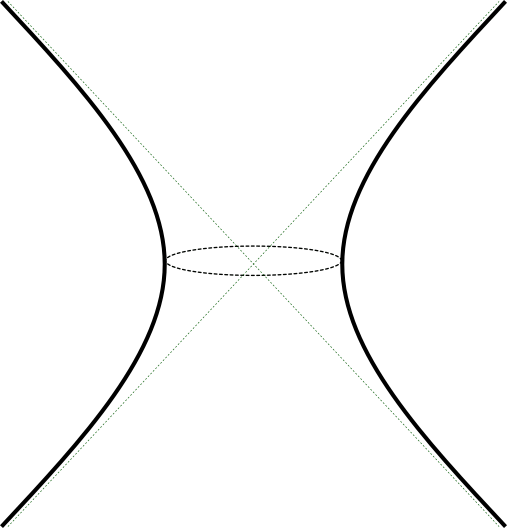
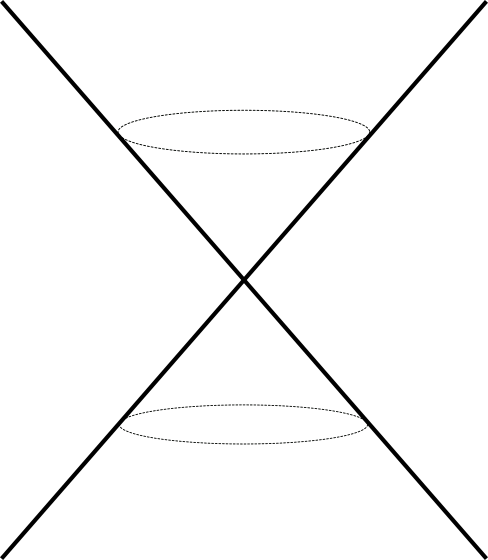
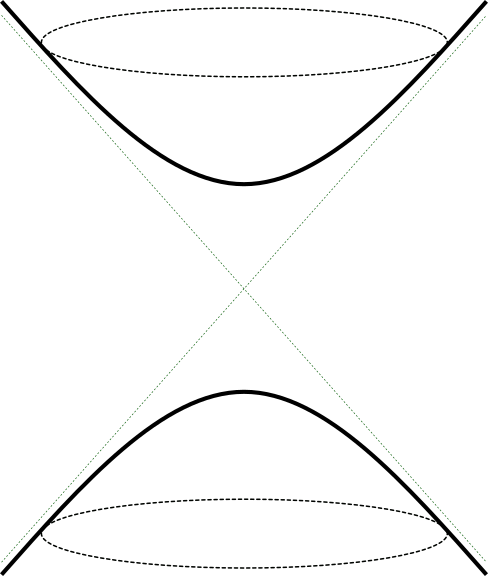
Consideremos el espacio $\R^{2,1}$ como $\R^3$ junto con la geometría dada por la forma cuadrádtica $Q(x,y,z) = x^2 + y^2 - z^2$ que tiene como simetrías lineales \begin{equation*} O(2,1) = \{A \in GL_3(\R) : A I_{2,1} A^t = I_{2,1} \}, \qquad I_{2,1} = \left(\begin{array}{cc} I_2 & 0 \\ 0 & -1 \end{array}\right), \end{equation*} con $I_2 \in GL_2(\R)$ matriz identidad. Los análogos a las esferas en esta geometría están dados por conjuntos de nivel de $Q$ para $1$, $0$ y $-1$ como muestra la figura 5.
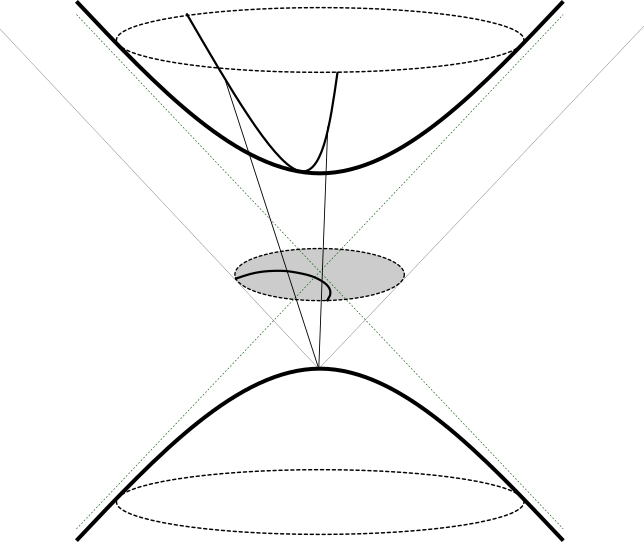
Mediante una proyección estereográfica, como ilustra la figura 6, tenemos una identificación de superficies \begin{equation*} \mathbb{D}^2 \cong \{ (x,y,z) \in \R^3 : Q(x,y,z) = -1, \quad z \mayorque 0 \} \end{equation*} que nos da un tercer modelo de superficie de curvatura constante $-1$, dando un isomorfismo de grupos $SL_2(\R) \cong SO(2,1)_0$ (donde el subíndice $0$ significa tomar la componente conexa que contiene la identidad).
Podemos modificar un poco la forma cuadrática de manera que si $Q'(x,y,z) = x^2 + y^2 - \sqrt{2} z^2$, entonces tiene grupo de simetrías \begin{equation*} G = \{ A \in GL_3(\R) : Q'(Ap) = Q'(p), \ \forall p \in \R^3 \} \cong O(2,1). \end{equation*}
Algo en lo que hay que tener cuidado es que aunque tengamos un subgrupo discreto $\Gamma \subset Iso(X)$ con cociente compacto $X / \Gamma$, no necesariamente la proyección $X \rightarrow X/\Gamma$ es un cubriente. Una forma de asegurar de que el cociente sí sea cubriente es pedir que la acción de $\Gamma$ en $X$ sea
Para entender por qué los puntos enteros
tomados en distintos modelos no siempre resultan en cocientes compactos como se vio en las secciones 1.2 y 2.1, primero hay que entender qué significa tomar puntos enteros
, relacionado con el concepto de $\Q$-estructura.
Un elemento $A \in SL_m(\R)$ se dice unipotente si existe $N \in \mathbb{N}$ tal que $(A - I)^N = 0$, esto es equivalente a que $A$ tenga sólo a $1$ como eigenvalor y por tanto, un elemento unipotente $A$ no trivial (es decir $A \neq I$) no será diagonalizable. El grupo discreto $SL_2(\Z)$ tiene elementos unipotentes como por ejemplo \begin{equation*} A = \left(\begin{array}{cc} 1 & 1 \\ 0 & 1 \end{array}\right) \end{equation*} que actúa en el semiplano $\mathbb{H}^2$ por traslaciones $A^n \cdot z = z + n$, de hecho, la presencia de este elemento es la razón por la cual el cociente $SL_2(\R) / SL_2(\Z)$ es no compacto como nos dice el criterio de Godement.
Este criterio también explica por qué funciona el ejemplo de la sección 2.1: Dada una forma cuadrática $Q$ en $\R^3$, denotemos por $SO(Q)$ las matrices en $SL_3(\R)$ que preservan $Q$. Dado que $\sqrt{2}$ es solución de una forma cuadrática sobre $\Q$, tenemos que el grupo de Galois $Gal(\Q[\sqrt{2}]/\Q) \cong \mathbb{Z}_2$ está generado por el elemento de orden 2, \begin{equation*} \sigma : \Q[\sqrt{2}] \rightarrow \Q[\sqrt{2}], \qquad \sigma(a + b \sqrt{2}) = a - b \sqrt{2}. \end{equation*} Podemos observar que $\sigma(x^2 + y^2 - \sqrt{2} z^2) = x^2 + y^2 + \sqrt{2} z^2$ y así el grupo \begin{equation*} K = SO(x^2 + y^2 + \sqrt{2} z^2) \cong SO(3) \end{equation*} es compacto. A pesar de que el grupo $G = SO(x^2 + y^2 - \sqrt{2} z^2)$ no está definido sobre $\Q$, sino sobre $\Q[\sqrt{2}]$, el grupo $\widehat{G} = G \times K$ sí está definido sobre $\Q$ y tenemos que \begin{equation*} \widehat{G}_\Z = \left\{ (g, \sigma(g)) \in G \times K : g \in G_{\Z[\sqrt{2}]} \right\}. \end{equation*} Dado que $SO(3)$ no tiene elementos unipotentes no triviales, pues toda matriz ortogonal es diagonalizable sobre $\mathbb{C}$, $K$ y por lo tanto $\widehat{G}$ tampoco tiene elementos unipotentes no triviales, así el criterio de Godement nos dice que el cociente $\widehat{G} / \widehat{G}_\Z$ es compacto. Por último, gracias a que $K$ es compacto y $\widehat{G}_\Z$ es discreto en $\widehat{G}$, entonces su proyección $G_{\Z[\sqrt{2}]} \subset G$ es discreta y tendrá cociente compacto $G / G_{\Z[\sqrt{2}]}$ que es justo lo que prometía la proposición 1.
En el procedimiento anterior, lo que se hizo fue: Dado $G \subset SL_m(\R)$ subgrupo cerrado, representarlo como ceros de polinomios con coeficientes sobre alguna extensión finita de $\Q$ de manera que todos sus conjugados de Galois fueran compactos. Esto es precisamente lo que hizo Armand Borel (1923-2003) para una familia de grupos bastante importantes conocidos como grupos semisimples para obtener:
Como ejemplo de lo anterior, podemos considerar $p,q \in \mathbb{N}$ y la forma hermitiana de signatura $(p,q)$ dada por $Q_{p,q}(z,w) = z_1 \overline{w_1} + ... z_p \overline{w_p} - z_{p+1} \overline{w_{p+1}} - ... - z_{p+q} \overline{w_{p+q}}$, sus correspondiente grupo de simetrías lineales \begin{equation*} G(\mathbb{F}) = \{ A \in SL_m(\mathbb{F}) : Q_{p,q}(A z,A w) = Q_{p,q}(z,w), \quad \forall \ z,w \in \mathbb{F}^{p+q} \} \end{equation*} son grupos semisimples*Más generalmente, productos finitos de estos grupos siguen siendo semisimples., los cuales se denotan según el anillo en cuestión por \begin{equation*} SO(p,q) = G(\R), \qquad SU(p,q) = G(\C), \qquad Sp(p,q) = G(\widehat{\Hip}), \end{equation*} donde denotamos por $\widehat{\Hip}$ el anillo de los cuaternios. Como caso particular, podemos observar que el grupo $SO(n,1)$ actúa transitivamente por isometrías en el espacio hiperbólico de dimensión $n$ denotado por $\mathbb{H}^n$ dándonos la identificación \begin{equation*} SO(n,1)_0 / SO(n) \cong \mathbb{H}^n, \end{equation*} usando el teorema 3 y el teorema 1 junto con la observación 2, obtenemos lo siguiente:
El grupo de Heisenberg $H$, descrito en la sección 1.2, es un ejemplo de un grupo que no es semisimple aunque como vimos también admite un subgrupo discreto con cociente compacto. En este caso, $H$ es nilpotente, es decir, existe un $n \in \mathbb{N}$ tal que $H_n = \{I\}$, donde $H_0 = H$, $H_{k+1} = [H_k,H_k]$ y el subgrupo conmutador está dado por \begin{equation*} [H,H] = \langle ghg^{-1}h^{-1} : g,h \in H \rangle. \end{equation*} Un grupo nilpotente $N$ admite subgrupos discretos $\Gamma \subset N$ tal que $N / \Gamma$ tiene volumen finito si y sólo si $N$ está definido sobre $\Q$, y en este caso, $N/\Gamma$ es inmediatamente compacto. En [Rag72, p. Remark 2.14] podemos encontrar un ejemplo de un grupo nilpotente $N$ dado por una extensión de grupos \begin{equation*} 1 \rightarrow \R^4 \rightarrow N \rightarrow \R^6 \rightarrow 1 \end{equation*} que no está definido sobre $\Q$ y por tanto no admite cocientes compactos.
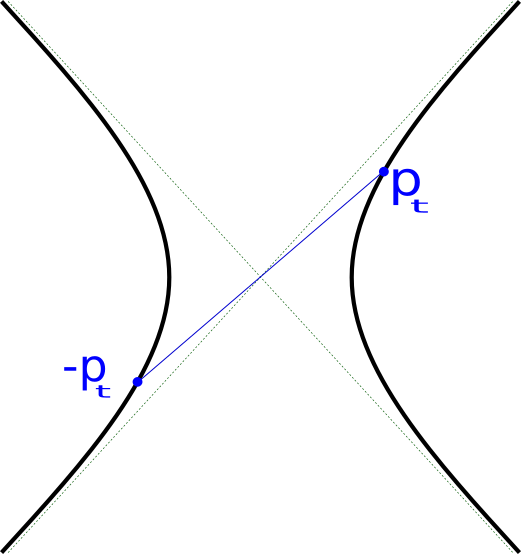
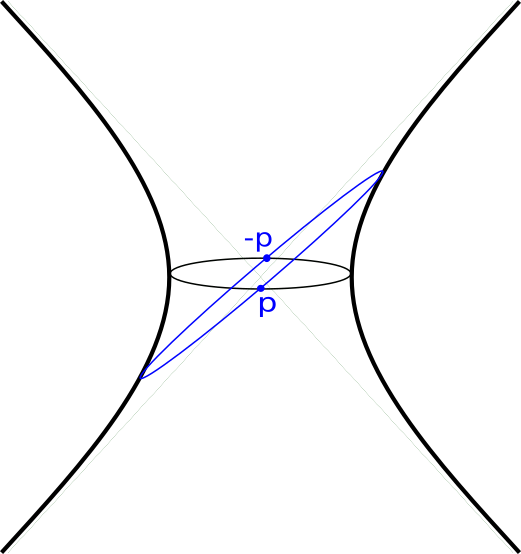
Cuando nos alejamos del mundo riemanniano, la situación se complica incluso más. Para ver esto, recordamos la geometría de $\R^{2,1}$ vista en la sección 2.1 y analizamos el ejemplo del hiperboloide de una hoja \begin{equation*} \Sigma^+ = \{ (x,y,z) \in \R^{2,1} : Q(x,y,z) = x^2 + y^2 - z^2 = 1 \}. \end{equation*} Ahora tangente a un punto $p \in \Sigma^+$, la forma cuadrática se ve como $Q = \zeta_1^2 - \zeta_2^2$ para cierta base $\{\zeta_1,\zeta_2\}$ de $T_p \Sigma^+$ que no es positiva y cuyo grupo de simetrías lineales está dado por las transformaciones hiperbólicas \begin{equation}\label{hyperb-matrix} g_t = \left(\begin{array}{cc} \textrm{cosh } t & \textrm{senh } t \\ \textrm{senh } t & \textrm{cosh } t \end{array}\right) \end{equation} que generan el grupo $SO(1,1)$, cuyo comportamiento se aprecia en la figura 7. La superficie $\Sigma^+$ es homogénea con el grupo de simetrías $SO(2,1)$ que está generado por rotaciones alrededor del eje $z$ y por transformaciones hiperbólicas del estilo ( 1) en secciones verticales del hiperboloide, por ejemplo \begin{equation*} \left(\begin{array}{ccc} 1 & 0 & 0 \\ 0 & \textrm{cosh } t & \textrm{senh } t \\ 0 & \textrm{senh } t & \textrm{cosh } t \end{array}\right) \in SO(2,1), \end{equation*} con lo que tenemos la identificación $\Sigma^+ \cong SO(2,1) / SO(1,1)$ y un comportamiento conocido como el fenómeno de Calabi-Markus.
Como consecuencia del fenómeno de Calabi-Markus, tenemos que si \begin{equation*} \pi: \Sigma^+ \rightarrow \widehat{\Sigma} \end{equation*} es un cubriente semirriemanniano ($\pi$ es una isometría local), entonces $\widehat{\Sigma}$ es no-compacto, pues su grupo fundamental $\Gamma = \pi_1(\widehat{\Sigma}) \subset SO(2,1)$ será finito y $\Sigma^+$ es no-compacto, en particular ¡no existen modelos compactos de esta geometría homogénea!
Como se vio en la sección anterior, otra situación en la que el grupo de simetrías es de Lie es en el contexto de variedades semirriemannianas [ONe83], [Kob95]. $X$ es una variedad semirriemanniana si la geometría está dada infinitesimalmente por una forma cuadrática no-degenerada \begin{equation*} \mathcal{G}_x : T_x X \times T_x X \rightarrow \R, \end{equation*} en cada punto $x \in X$. Al ser no-degenerada tendremos que una base $\{\zeta_1,...,\zeta_n\}$ de $T_x X$ podemos expresar la forma cuadrática como \begin{equation*} \mathcal{G}_x = \zeta_1^2 + ... + \zeta_p^2 - \zeta_{p+1}^2 - ... - \zeta_n^2. \end{equation*} A la pareja de números $(p,n-p) \in \N^2$ se le conoce como la signatura de la forma cuadrática $\mathcal{G}_x$, y si $X$ es conexa, entonces ésta es la misma en todo punto.
Dada una pareja $p,q \in \N$, tenemos modelos homogéneos de geometría semirriemanniana de curvatura constante y signatura $(p,q)$ que denotamos por $X_{p,q}^k$ y están dados respectivamente por
Hay varios ejemplos para los que sabemos que existen modelos compactos, por ejemplo los toros semirriemannianos $\mathbb{T}^{p,q} = \R^{p,q} / \Z^{p,q}$ o los modelos riemannianos que es cuando $p= 0$ o $q=0$. Así mismo, el fenómeno de Calabi-Markus de la sección anterior se puede extender a dimensiones mayores y ver que $SO(p+1,1)/SO(p,1)$ nunca admite modelos compactos.
Un ejemplo más para el que conocemos la existencia de modelos compactos es el hiperboloide complejo
\begin{equation*} X = \{ (z_1,...,z_n,w) \in \C^{n,1} = z_1 \overline{z_1} + ... + z_n \overline{z_n} - w \overline{w} = 1\}. \end{equation*}
Si olvidamos la multiplicación compleja, es decir, si consideramos el isomorfismo de espacios vectoriales reales $\C_\R^{n,1} \cong \R^{2n,2}$, tenemos la doble identificación
\begin{equation*} X \cong SO(2n,2) / SO(2n,1) \cong SU(n,1) / SU(n), \end{equation*}
en donde $SU(n,1)$ es semisimple y $SU(n)$ es compacto, por lo que los teoremas 3 y 1 se combinan con la observación 2 para darnos un modelo compacto de esta geometría. Se tiene la siguiente conjetura (Space Form problem en [KY05]) que nos dice que de alguna manera los únicos espacios de curvatura constante que admiten modelos compactos son los que podemos obtener por realificar
estructuras reales, complejas, cuaterniónicas u octoniónicas:
| $p$ | $\N$ | 0 | 1 | 3 | 7 |
| $q$ | 0 | $\N$ | $2\N$ | $4\N$ | 8 |
| $p$ | 0 | $\N$ | $2\N$ | $4\N$ | 8 |
| $q$ | $\N$ | 0 | 1 | 3 | 7 |
Por último, mencionamos otra forma de ver que ciertos espacios homogéneos no admiten cocientes compactos, ahora con la ayuda de la dinámica. Para esto recordamos que una acción de un grupo $\Gamma$ en un espacio $X$ por transformaciones medibles es ergódica si los únicos subconjuntos $\Gamma$-invariantes son de medida cero o de medida total. El siguiente resultado nos da muchos ejemplos interesantes de acciones ergódicas en el contexto que hemos venido mencionando [Zim84].
Tenemos de manera inmediata dos consecuencias del teorema anterior:
Podemos hacer esto mucho más explícito, consideremos la inclusión de grupos \begin{equation*} SO(3,2) \times SO(3) \rightarrow SO(3,5), \qquad (A,B) \mapsto \left(\begin{array}{cc} A & 0 \\0 & B \end{array}\right), \end{equation*} y $\Gamma \subset SO(3,5)$ subgrupo discreto libre de torsión con cociente $SO(3,5) / \Gamma$ de volumen finito (teorema 3 y teorema 1 nos ayudan a tener ejemplos de esto). Dado que los grupos $SO(3,2)$ y $SO(3)$ conmutan, tenemos la acción izquierda por multiplicación \begin{equation*} SO(3,2) \curvearrowright SO(3) \backslash SO(3,5) / \Gamma \end{equation*} que por el teorema 5 tiene órbitas densas. Este comportamiento dinámico da indicios de la siguiente conjetura que es un caso muy particular de una serie de conjeturas conocida como el programa de Zimmer sobre rigidez de acciones de grupos simples no-compactos.
Agradezco al apoyo por parte del proyecto CONACyT CB2016-283988-F, así como al proyecto CONACyT/FORDECyT 265667. Agradezco a Jesús Núñez Zimbrón por recomendarme participar con esta nota en la revista Motivos Matemáticos, así como al equipo editorial por las valiosas correcciones y recomendaciones.