
En este manuscrito discutimos una de las contribuciones que la teoría de los sistemas dinámicos ofrece al entendimiento del crecimiento de una población de individuos con recursos limitados. En este contexto, exploramos brevemente algunas de las ideas que permiten entender dos mecanismos de vital importancia en ecología: la competencia y la interacción con los recursos del medio. El enfoque que seguiremos consistirá en la exposición de los resultados clave publicados en [1] por R. Dilao y T. Domingos para la dinámica de una generalización del modelo de Leslie. Asimismo, presentamos los resultados de algunos experimentos numéricos cuando se considera un retraso de la variable de evolución en la dinámica del crecimiento de los recursos y una dinámica de competencia simple entre los miembros de la población.
Las matemáticas juegan un papel clave en el quehacer científico. Los métodos y teorías que de ella emanan, no solamente proveen de capacidad de predicción, sino que también pueden ayudar en el diseño de experimentos, o bien, arrojar luz en el entendimiento de fenómenos naturales que son inaccesibles para las ciencias experimentales mediante la experimentación in silico.
Una de las ramas de la ciencia que se ha visto beneficiada por las matemáticas en el último siglo es, sin duda, la biología. Esta es posiblemente una de las consecuencias más relevantes de la labor del zoólogo escocés D'Arcy Thompson, quien a principios del siglo xx, al establecer un especial énfasis en el papel que las leyes de la física juegan en el crecimiento de los organismos y el distintivo impacto que las matemáticas tienen en el entendimiento de estos fenómenos, se convirtió en uno de los pioneros de las biomatemáticas. Como puede verse en su libro On Growth and Form, véase [2], este énfasis se ve reflejado en el siguiente fragmento:
En las últimas décadas, ha habido un creciente grupo de especialistas en las distintas áreas del conocimiento humano que ha orientado sus intereses al entendimiento de fenómenos de origen biológico. Sin embargo, aunque el camino por recorrer en el desarrollo de una descripción completa de estos fenómenos está aún lejos de alcanzarse, existen avances de especial importancia desde el punto de vista de las matemáticas; por ejemplo, en la modelación matemática de fenómenos en ecología y en fisiología; véanse, por ejemplo, los aportes recolectados en [3,4,5] y en [6], respectivamente. En este sentido, particularmente, las ideas de Alan M. Turing sentaron las bases de la teoría de la morfogénesis, como puede verse en su trabajo seminal en el área [7]. Que aunque aún están en controversia en la comunidad científica, han sido fundamentales para el diseño de nuevos experimentos y, más aún, han puesto en escena las consecuencias de las interacciones de largo y corto alcance en una amplia variedad de procesos biológicos; véanse, por ejemplo, [8,9,10]. De este modo, no solamente la biología se ha visto influencia favorablemente (e. g. [11]), sino que, como consecuencia del planteamiento de problemas de índole biológica, éstos han dado origen a problemas de interés matemático (e. g. [12]). Un beneficio claro de esta interacción de disciplinas puede observarse en la teoría de formación de patrones, donde una creciente comunidad de matemáticos ha hecho contribuciones de especial relevancia, e. g. [13,14]. En el primero se discute el encuentro entre una teoría proveniente de los sistemas dinámicos y las ideas de Turing para mostrar las consecuencias de un mecanismo dinámico que produce patrones, los cuales tienen las características esenciales de estructuras encontradas en observaciones de algunas interacciones bioquímicas; por otro lado, en el manuscrito de M. Ward principalmente se hace un recuento histórico en el que el análisis asintótico ha contribuido en problemas que surgieron a partir de las ideas de Turing.
En un contexto distinto, la discusión de algunos ejemplos donde teorías, herramientas y métodos matemáticos han arrojado luz a la descripción y al entendimiento de distintos procesos biológicos puede verse en la publicación de P. H. Leslie, véase [15].
En este ensayo nos centraremos en un problema donde se arrojan algunas ideas que son clave para el análisis del crecimiento de una población de individuos. Esta perspectiva en la cual estos planteamientos están orientados son capturados por la teoría de los sistemas dinámicos (discretos). Este enfoque, desde el punto de vista de la modelación matemática, consiste en el análisis de las relaciones de correspondencia entre variables de estado y un operador de evolución y el conjunto de parámetros que caracterizan el fenómeno en estudio. La exposición que se persigue no es formal, sino que está principalmente orientada a ilustrar el tipo de herramientas y métodos que tienen como objetivo principal proporcionar respuestas a planteamientos de origen biológico, particularmente ecológico.
El estudio del crecimiento de las poblaciones es uno de los pilares de la ecología. A partir de su descripción es posible entender dinámicas relacionadas con la interacción entre especies, por ejemplo, la cooperación y la competencia. De esta manera, la capacidad de predicción de las consecuencias de estas interacciones es fundamental. Por lo tanto, desde el punto de vista de la modelación matemática, la naturaleza de las interacciones determina el objeto matemático que ofrecerá respuesta a las incógnitas del fenómeno en estudio. En otras palabras, determinar la validez de los resultados que son obtenidos dependen del enfoque elegido. En esencia, el modelo propuesto debe tener dos características principales: (i) simpleza y (ii) generalidad. En particular, un modelo de crecimiento de poblaciones captura los ingredientes principales de la interacción que se pretende analizar y, a su vez, debe ser tratable matemáticamente; es decir, los ingredientes que se capturan en el modelo matemático son clave para el estudio del fenómeno.
Los modelos de poblaciones más sencillos y sin embargo más relevantes son aquellos que poseen las siguientes propiedades:
El modelo de Leslie es una propuesta que incorpora los ingredientes arriba señalados. La deducción de este modelo consiste en considerar una población de individuos que se encuentra dividida por una clasificación según su edad; los intervalos que determinan las clases de edad pueden considerarse del mismo tamaño. Esto es, si $E$ es el parámetro de edad que determina la unidad de tiempo y se tienen $n$ clases, entonces $E/n$ corresponde al tamaño de cada uno de los intervalos para cada clase. En otras palabras, la $j$-ésima clase tiene un intervalo de edad
\begin{gather}\label{eq:interv} I_j=\left[\frac{(j-1)E}{n},\frac{jE}{n}\right]\,, \quad \textrm{para} \quad j=1,\dots,n\,. \end{gather} Por otro lado, $\vectorr{x}_0\in\mathbb{R}^n$ es el vector inicial de distribución de la población según la edad; es decir, la componente $x_{j0}$ corresponde a la población inicial de individuos en la $j$-ésima clase. Al suponer que el tiempo en el cual los individuos de una clase migran a la siguiente corresponde al tamaño del intervalo $I_j$ para cada clase, entonces la variable de evolución es definida como \begin{gather*} t_k=\frac{kE}{n}\,, \quad \textrm{donde} \quad k=1,\dots,n\,; \end{gather*}de este modo, $\vectorr{x}_k^T=[x_{1k},\dots,x_{nk}]$ es el vector de distribución del número de individuos en el tiempo $t_k$, donde $x_{jk}$ indica el número de individuos en la $j$-ésima clase al tiempo $t_k$.
Si todos los individuos en la $(j+1)$-ésima clase al tiempo $t_{k+1}$ estuvieron en la $j$-ésima clase al tiempo $t_k$, es posible suponer que
Consideremos que al tiempo $t_{k+1}$ los miembros de la primera clase son descendientes de aquellos que nacieron entre el tiempo $t_{k}$ y el tiempo $t_{k+1}$; es decir,
\begin{gather}\label{eq:sist01} x_{1(k+1)}=\beta_1x_{1k}+\beta_2x_{2k}+\cdots+\beta_nx_{nk}\,.\tag{2a} \end{gather} Por el otro lado, el número de individuos en la $(j+1)$-ésima clase, con $j=1,\dots,n-1$, al tiempo $t_{k+1}$ son aquellos que en la $j$-ésima clase al tiempo $t_{k}$ sobreviven al tiempo $t_{k+1}$; esto conduce a que \begin{gather}\label{eq:sist02} x_{(j+1)(k+1)}=\alpha_jx_{jk}\,.\tag{2b} \end{gather}De esta forma, a partir del sistema \eqref{eq:sist}, obtenemos el sistema de Leslie
\begin{gather}\label{eq:leslie} \underbrace{\vecolcinco{x_{1(k+1)}}{x_{2(k+1)}}{x_{3(k+1)}}{\vdots}{x_{n(k+1)}}}_{\displaystyle \vectorr{x}_{k+1}}=\underbrace{\left[\begin{array}{ccccc} \displaystyle \beta_1 & \displaystyle \beta_2 &\displaystyle \beta_3 & \displaystyle \cdots &\displaystyle \beta_n \\ \\[-2.5ex] \displaystyle \alpha_1 & \displaystyle 0 & \displaystyle 0 & \displaystyle \cdots &\displaystyle 0 \\ \\[-2.5ex] \displaystyle 0 & \displaystyle \alpha_2 &\displaystyle 0 & \displaystyle \cdots &\displaystyle 0 \\ \\[-2.5ex] \displaystyle \vdots &\displaystyle \ddots & \displaystyle \ddots &\displaystyle \ddots &\displaystyle \vdots \\ \\[-2.5ex] \displaystyle 0 & \displaystyle \cdots & \displaystyle 0 & \displaystyle \alpha_{n-1} &\displaystyle 0 \end{array}\right]}_{\displaystyle \vectorr{L}}\underbrace{\vecolcinco{x_{1k}}{x_{2k}}{x_{3k}}{\vdots}{x_{nk}}}_{\displaystyle \vectorr{x}_{k}}\,, \end{gather}donde $\vectorr{L}$ se conoce como la matriz de Leslie. De este modo, al ser $\vectorr{L}$ una matriz constante, el vector de distribuciones de edad de la población al tiempo $t_k$ está dada por la $k$-ésima iteración de esta matriz del vector inicial de distribuciones, es decir: $\vectorr{x}_{k}=\vectorr{L}^k\vectorr{x}_0$.
Con el fin de hacer un bosquejo de la dinámica de la población, calculamos las raíces del polinomio característico de la matriz $\vectorr{L}$, las cuales están determinados por las raíces de este polinomio característico
\begin{gather}\label{eq:polcarac} P_n(\lambda):=\det{\left(\vectorr{L}-\lambda\vectorr{I}\right)}=\left(-1\right)^n\left(\lambda^n-\beta_1\lambda^{n-1}-\beta_2\alpha_1\lambda^{n-2}-\cdots-\beta_n\alpha_1\alpha_2\cdots\alpha_{n-1}\right)\,. \end{gather}Notemos que si los individuos en la $n$-ésima clase son fértiles, i. e. $\beta_n\mayorque 0$, entonces $\lambda\neq0$. En consecuencia, definimos la función
\begin{gather}\label{eq:q} Q_n(\lambda):=\frac{P_n(\lambda)}{\lambda^n}\,. \end{gather}Debido a que $Q_n(\lambda)$ es monótona decreciente para $\lambda\mayorque 0$, el teorema del valor intermedio garantiza que existe un único valor $\lambda_1\mayorque 0$ tal que $Q_n(\lambda_1)=1$. En otras palabras, el valor propio $\lambda_1$ es de multiplicidad uno. Más aún, observemos que si $\vectorr{u}_1$ es el vector propio correspondiente a $\lambda_1$, obtenemos que $\vectorr{L}\vectorr{u}_1=\lambda_1\vectorr{u}_1$, donde $\vectorr{u}_1^T=[u_{11},\dots,u_{n1}]$, es decir
\begin{gather*} \beta_1u_{11}+\beta_2u_{21}+\cdots+\beta_nu_{n1}=\lambda_1u_{11} \quad \textrm{y} \quad \alpha_{j}u_{j1}=\lambda_1u_{j1}\,, \quad \textrm{para} \quad j=1,\dots,n-1\,. \end{gather*}A partir de estas ecuaciones y que $\lambda_1$ satisface la ecuación
\begin{gather}\label{eq:qcond} \frac{\beta_1}{\lambda_1}+\frac{\beta_2\alpha_1}{\lambda_1^2}+\cdots+\frac{\beta_n\alpha_1\alpha_2\cdots\alpha_{n-1}}{\lambda_1^n}=1\,, \end{gather}lo valores de las componentes del único vector propio $\vectorr{u}_1$ están dados por
\begin{gather*} u_{11}=1\,, \quad \textrm{y} \quad u_{j1}=\frac{1}{\lambda_1^{j-1}}\prod\limits_{m=1}^{j-1}\alpha_{m}\,, \quad \textrm{para} \quad j=2,\dots,n\,. \end{gather*}Este resultado puede escribirse de la siguiente manera:
Ahora, consideremos los valores propios distintos de $\lambda_1$. Para cualquier índice $j\neq1$, el valor propio correspondiente puede escribirse en su forma polar compleja $\lambda_j=\left|\lambda_j\right|e^{\displaystyle i\theta}$; a partir de \eqref{eq:q} tenemos que
\begin{gather*} \left|Q_n\left(\left|\lambda_j\right|e^{\displaystyle i\theta}\right)\right|\geq1\,, \end{gather*}lo cual quiere decir que $\left|\lambda_j\right|\leq\lambda_1$. En consecuencia, formulamos el
Los resultados 2.1 y 2.2 indican que la distribución de edad de la población total cuando el tiempo tiende a infinito es determinada por $\lambda_1$ en la dirección del vector propio $\vectorr{u}_1$, siempre que la $n$-ésima clase esté conformada por individuos fértiles y cuando las clases de la población son establecidas en términos de los intervalos dados en \eqref{eq:interv}. Dicho de otra forma, el parámetro $E$ controla esta clasificación, lo cual quiere decir que es posible analizar el crecimiento de cualquier población de individuos discriminando las clases de individuos que no son fértiles. En consecuencia, la dinámica del sistema \eqref{eq:leslie} es tal que la condición inicial $\vectorr{x}_0$ tiende a la extinción o a la explosión demográfica, si $\lambda_1$ es menor o mayor que 1.
Notemos que, a partir de \eqref{eq:qcond}, la condición
\begin{gather}\label{eq:gamma} \rho:=\beta_1+\beta_2\alpha_1+\cdots+\beta_n\alpha_1\alpha_2\cdots\alpha_{n-1}=1\,, \end{gather}determina que la población tiene un comportamiento asintótico acotado. El parámetro $\rho$ se conoce como el número de reproducción neta inherente (véase [16]) y determina si la población, en términos del modelo lineal de Leslie \eqref{eq:leslie}, se extingue o crece sin cota; en otras palabras, $\rho\mayorque 1$ o $\rho\menorque 1$, si $\lambda_1\mayorque 1$ o $\lambda_1\menorque 1$, respectivamente.
A continuación, incorporaremos la dinámica correspondiente al crecimiento de recursos, los cuales son considerados limitados por sus características intrínsecas; por ejemplo, la resistencia a condiciones adversas o la rapidez de crecimiento.
El modelo de Leslie consiste en una descripción lineal que no solamente arroja resultados para el entendimiento del crecimiento de poblaciones de individuos, sino que no toma en cuenta factores de especial relevancia en el contexto, por ejemplo, del cambio climático. Con el fin de entender escenarios más realistas, exponemos el bosquejo del estudio de una población del tipo Leslie sujeta a la dinámica de crecimiento de los recursos y su interacción con los individuos de la población. Es decir, los recursos no solamente son consumidos por la población, cuya consecuencia es limitar su disponibilidad, sino que su dinámica captura las características esenciales del crecimiento logístico (véase [17]). Interacciones de este tipo son de especial relevancia en la ecología debido a que la supervivencia de los seres vivos depende directamente de los recursos (véase [18]).
A continuación haremos un breve resumen del análisis y algunos resultados que Dilao y Domingos en [1] obtienen al analizar un sistema generalizado del modelo de Leslie. A diferencia del sistema \eqref{eq:leslie}, el modelo propuesto por estos autores tiene la característica de ser denso-dependiente, es decir, la relación de correspondencia depende de las variables de estado. En otras palabras, $\vectorr{L}$ depende de los recursos al tiempo $t_k$, denotada por $R_k$ y, por tanto, de la población misma.
En los ingredientes principales para la deducción de este modelo, primero, suponemos que la fracción de individuos que sobrevive en cada clase depende monótonamente de la densidad de recursos, es decir, $\alpha_j=\alpha_j(R_k)$. Tomamos en cuenta que el comportamiento asintótico de este parámetro captura la fuerte dependencia de la población y los recursos, es decir: (i) $\alpha_j(R_k)\to0$ cuando $R_k\to0$ y (ii) $\alpha_j(R_k)\to1$ cuando $R_k\to\infty$.
Por otro lado, el cambio de la densidad de los recursos en el tiempo $t_{k+1}$ depende de la densidad de los recursos mismos y de la población total en el tiempo $t_{k}$; dicho de otro modo,
\begin{gather}\label{eq:recu} R_{k+1}=f\left(R_k,X_k\right)\,, \end{gather}donde $X_k=\sum_{j=1}^nx_{jk}$ es la población total en el tiempo $t_k$. La relación de correspondencia que captura la interacción dinámica de los recursos y la población en todas las clases está dada por la función $f$, de tal manera que ésta tiene dos puntos fijos: (i) el origen $(0,0)$, el cual representa ausencia de recursos y de la población; (ii) el punto $(K,0)$, cuya interpretación es la saturación de recursos del medio en ausencia de individuos. De esta manera, en ausencia de la población, consideraremos que los recursos aumentarán y, por otro lado, el medio se saturará a una cantidad $K$; este parámetro es conocido como capacidad de carga e indica la cantidad de recursos que el medio tiene para sostener una población. Notemos que el primer punto fijo es repulsor y el segundo es atractor; es decir, la razón de cambio de $f$ respecto a $R_k$ en los puntos de interés satisface que
\begin{gather}\label{eq:fcond} f_{R_k}(0,0)\mayorque 1 \quad \textrm{y} \quad f_{R_k}(K,0)\menorque 1\,. \end{gather}Estas dos condiciones representan que, en ausencia de consumidores, los recursos saturarán el medio.
Junto con las hipótesis \eqref{eq:fcond} para la ecuación \eqref{eq:recu}, el sistema \eqref{eq:leslie} toma la forma
\begin{gather}\label{eq:lesliemod01} \vecoldos{\vectorr{x}_{k+1}}{R_{k+1}}=\vecoldos{\vectorr{L}\left(R_k\right)\vectorr{x}_k}{f\left(R_k,X_k\right)}\,,\tag{10a} \end{gather} donde \begin{gather}\label{eq:lesliemod02} \vectorr{L}\left(R_k\right)=\left[\begin{array}{ccccc} \displaystyle \beta_1 & \displaystyle \beta_2 &\displaystyle \beta_3 & \displaystyle \cdots &\displaystyle \beta_n \\ \\[-2.5ex] \displaystyle \alpha_1(R_k) & \displaystyle 0 & \displaystyle 0 & \displaystyle \cdots &\displaystyle 0 \\ \\[-2.5ex] \displaystyle 0 & \displaystyle \alpha_2(R_k) &\displaystyle 0 & \displaystyle \cdots &\displaystyle 0 \\ \\[-2.5ex] \displaystyle \vdots &\displaystyle \ddots & \displaystyle \ddots &\displaystyle \ddots &\displaystyle \vdots \\ \\[-2.5ex] \displaystyle 0 & \displaystyle \cdots & \displaystyle 0 & \displaystyle \alpha_{n-1}(R_k) &\displaystyle 0 \end{array}\right]\,,\tag{10b} \end{gather}junto con las siguientes propiedades:
De este modo, la función de crecimiento de los recursos por contacto con la población se escribe como $f(R_k,X_k)=\psi(R_k)\varphi(X_k)$, donde $\psi(R_k)$ es la función de crecimiento de los recursos y $\varphi(X_k)$ es la distribución de probabilidad de encuentros de la población con los recursos; esta última es considerada de la forma de Ricker (véase [19] para mayores detalles), i. e. $\varphi(X_k)=e^{\displaystyle-\mu X_k}$, donde $\mu$ es la razón de consumo y puede considerarse, bajo un cambio de escala adecuado, idénticamente a 1.
Debido a que las condiciones en (i) y (ii) son satisfechas por la ecuación logística para el crecimiento de recursos, se tiene que
\begin{gather}\label{eq:logis} \psi(R_k)=\frac{\gamma KR_k}{\left(\gamma-1\right)R_k+K}\,, \end{gather}donde $\gamma\geq1$ es la razón de crecimiento intrínseco de los recursos.
Notemos que el parámetro $\alpha_j$ indica la transición de la $j$-ésima clase a la $(j+1)$-ésima clase y, a su vez, depende de los recursos, lo cual señala que es posible suponer que este parámetro toma la forma de una distribución de probabilidad de un proceso de natalidad y mortandad (véase [20]), i. e.
\begin{gather*} \alpha_j(R_k)=\frac{\delta_jR_k}{1+\delta_jR_k}\,, \quad j=2,\dots,n\,, \end{gather*}donde $\delta_j$ es la razón de transición debida a la cantidad de recursos de la $j$-ésima clase a la $(j+1)$-ésima clase.
A continuación, aunque el objetivo de este ensayo no es reproducir un análisis riguroso, sino mostrar algunos experimentos numéricos haciendo dos consideraciones relevantes de interés dinámico y, en el contexto de la presente exposición, ecológico: (i) crecimiento de recursos debido a contribuciones en dos tiempos distintos sin y con retraso; (ii) competencia entre clases de la misma población.
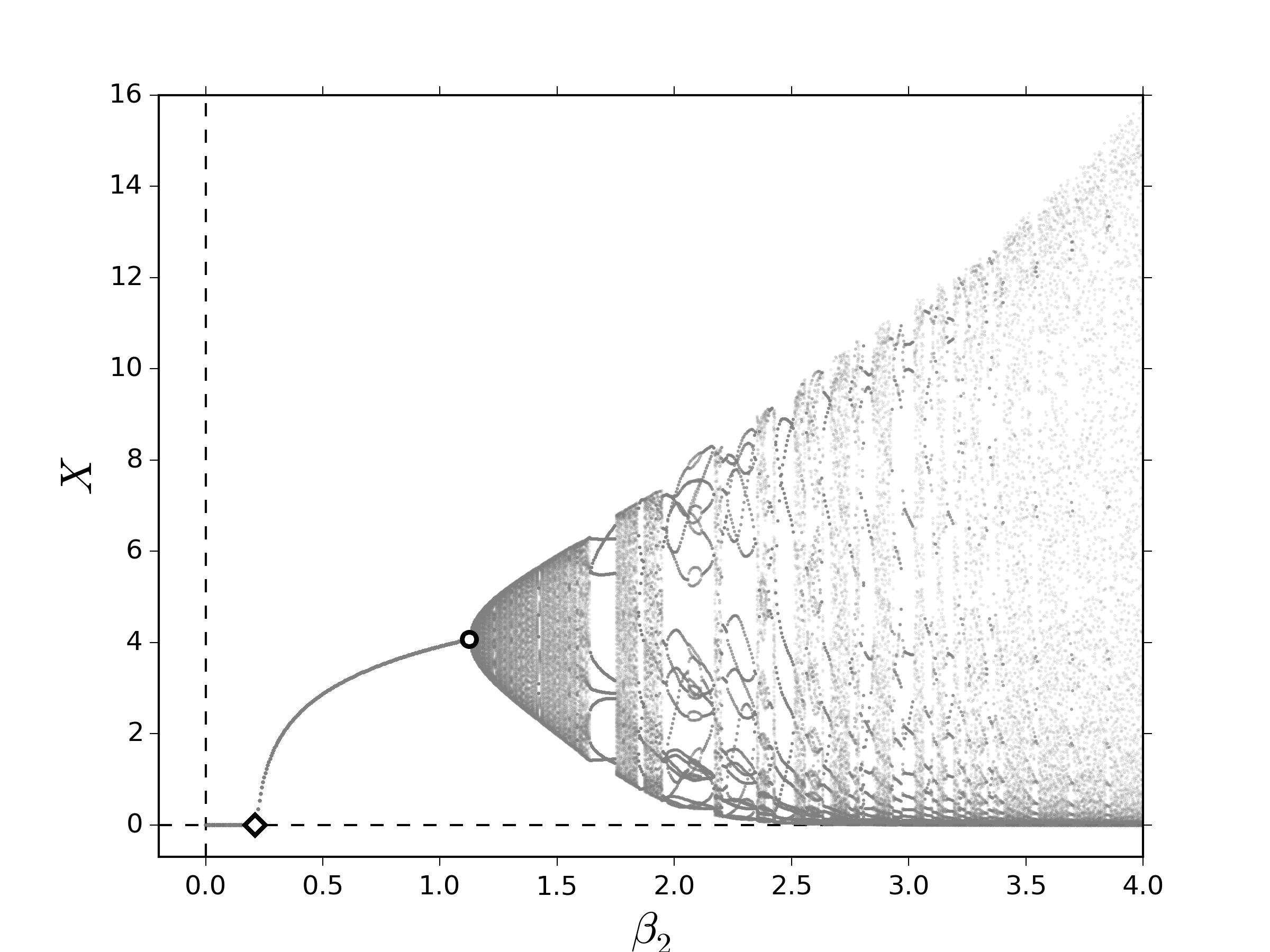
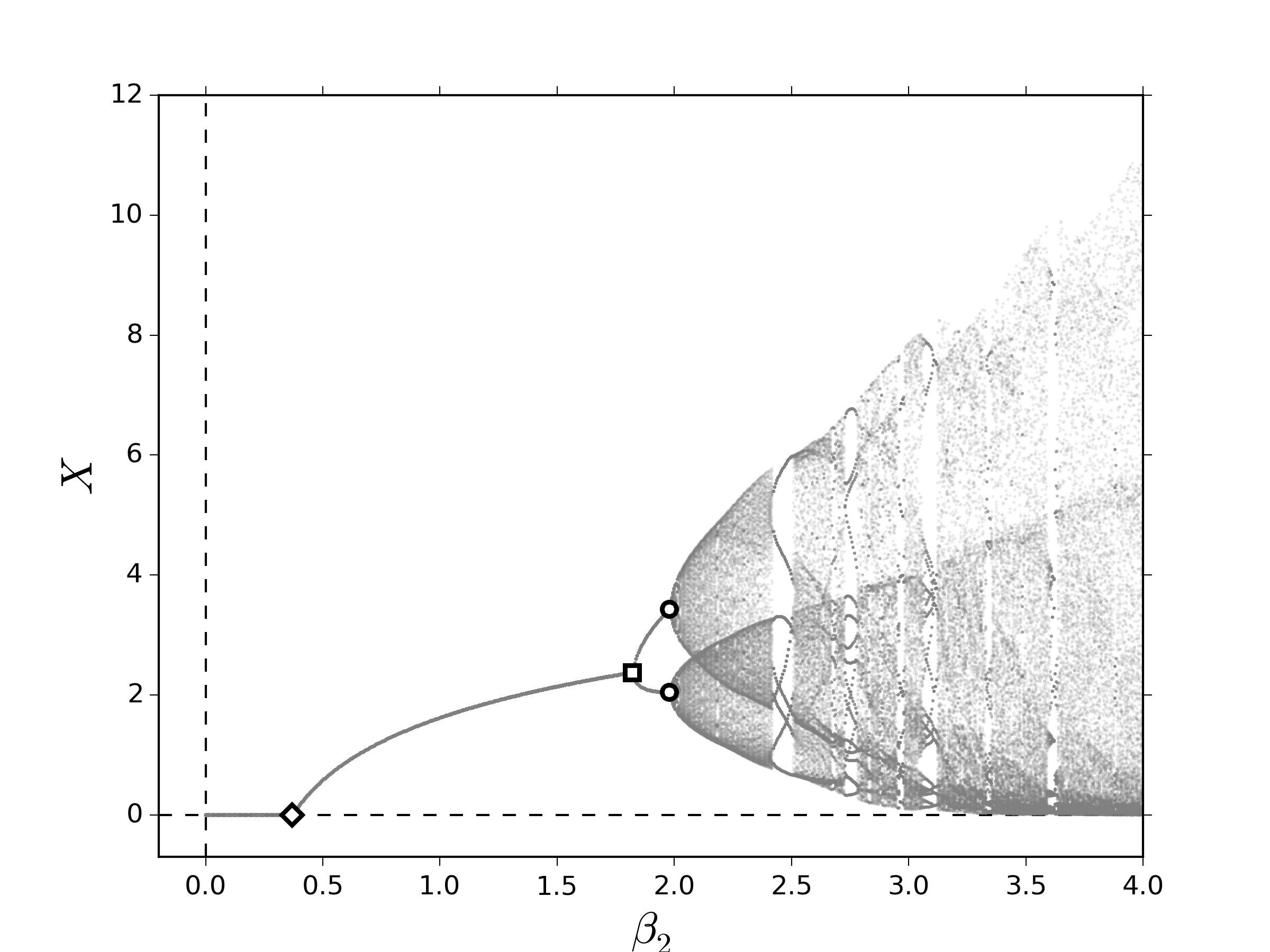
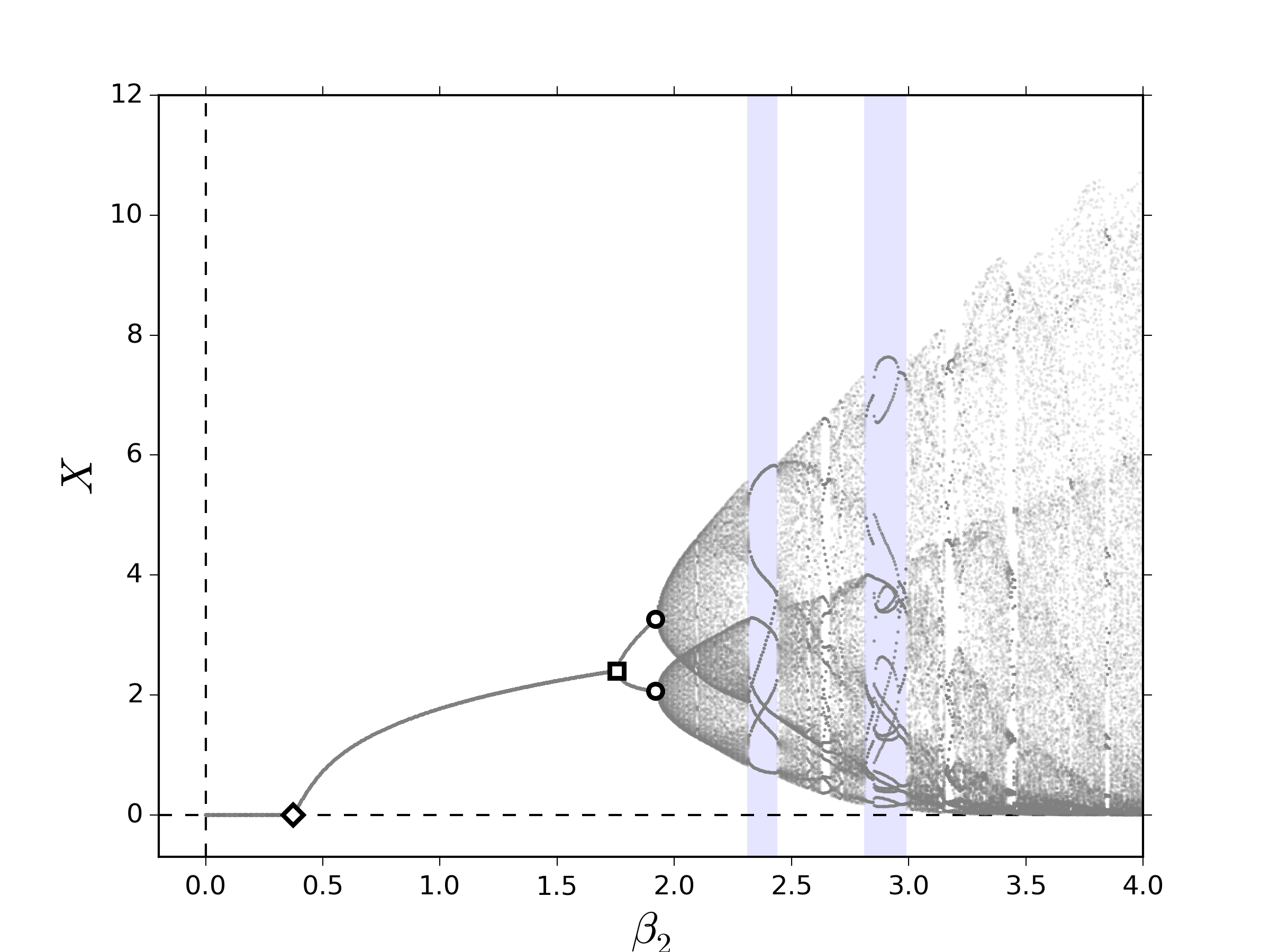
Primero, consideremos el caso bosquejado en la subsección 2.1, el cual es presentado detalladamente en [1]. En la figura 1 se muestran los diagramas de bifurcación al variar lentamente el número promedio de descendientes correspondiente a los individuos de la segunda clase, $\beta_2$, y tomamos como medida la población total asintótica, $X:=\lim\limits_{k\to\infty} X_k$. Tomaremos en cuenta que $\beta_1=0$, es decir, la clase de individuos que se encuentran en edad fértil se encuentran a partir de la segunda clase. En los dos escenarios que consideramos, observamos una sucesión de bifurcaciones que conducen a comportamientos cuasi-periódicos, las cuales corresponden a las órbitas cuyo período es irregular:
Los eventos dinámicos encontrados en la figura 1 ocurren cuando el valor propio dominante, definido en el resultado 2.2, cruza la frontera el disco unitario de tal modo que origina: (i) una bifurcación TS: $\lambda_1=1$, (ii) una bifurcación PD: $\lambda_1=-1$ y (iii) una bifurcación NS: $\lambda_1=\exp\left(im\theta\right)$, para $\theta\in\mathbb{R}\setminus\left\{\displaystyle 2\pi \nu/m\right\}_{\displaystyle\nu\in\mathbb{Z}}$. Una discusión detallada de estos eventos dinámicos puede encontrarse por ejemplo en [21,22].
Con el fin de mostrar algunas consecuencias dinámicas producidas por la inclusión de un retraso en la dinámica que en este manuscrito discutimos, a continuación presentamos algunos experimentos numéricos.
Como puede verse en \eqref{eq:logis}, el crecimiento de los recursos sigue un comportamiento logístico, donde la razón de crecimiento intrínseco de los recursos modela la rapidez con la que los recursos crecen. En otras palabras, $\gamma$ se interpreta como la razón de la capacidad que tienen los recursos para recuperarse debido a características propias del medio donde se reproducen. De este modo, esta razón puede verse afectada por los recursos mismos. En otras palabras, la rapidez con la cual estos recursos crecen dependen de los recursos en el tiempo $t_k$, pero también debido a los recursos en el tiempo $t_{k-1}$. Esta dependencia proviene de considerar el crecimiento de comunidades de plantas como el maíz, la sandía o el frijol, las cuales son plantas que germinan, reproducen y mueren en el transcurso de un año; para una discusión introductoria a la dinámica de poblaciones de plantas estacionales, véase [23]. En este sentido, podemos suponer el caso más sencillo, i. e. $\gamma(R_{k-1})=\tilde\gamma R_{k-1}$. De esta manera, el crecimiento de los recursos \eqref{eq:logis} está dada por
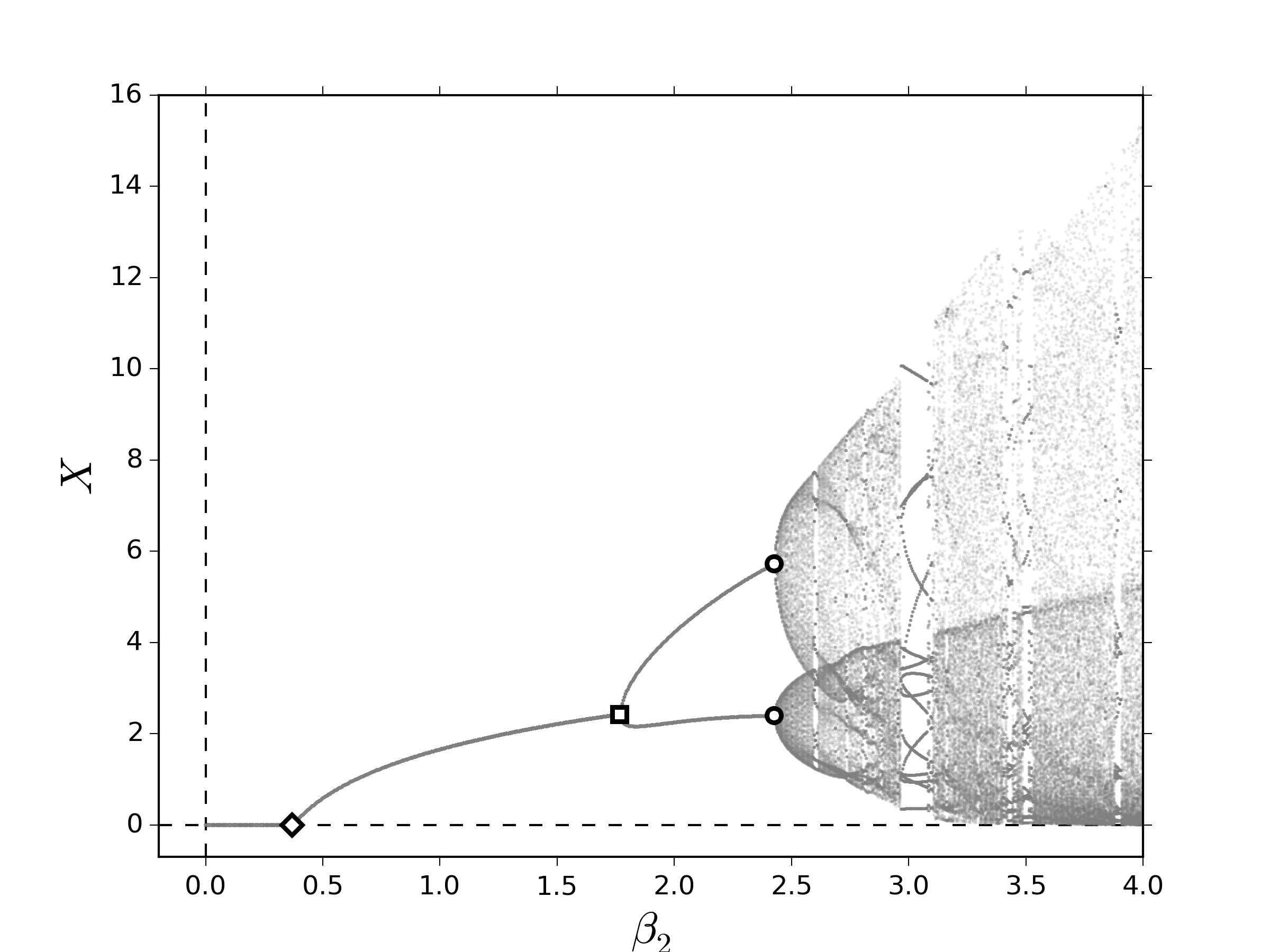
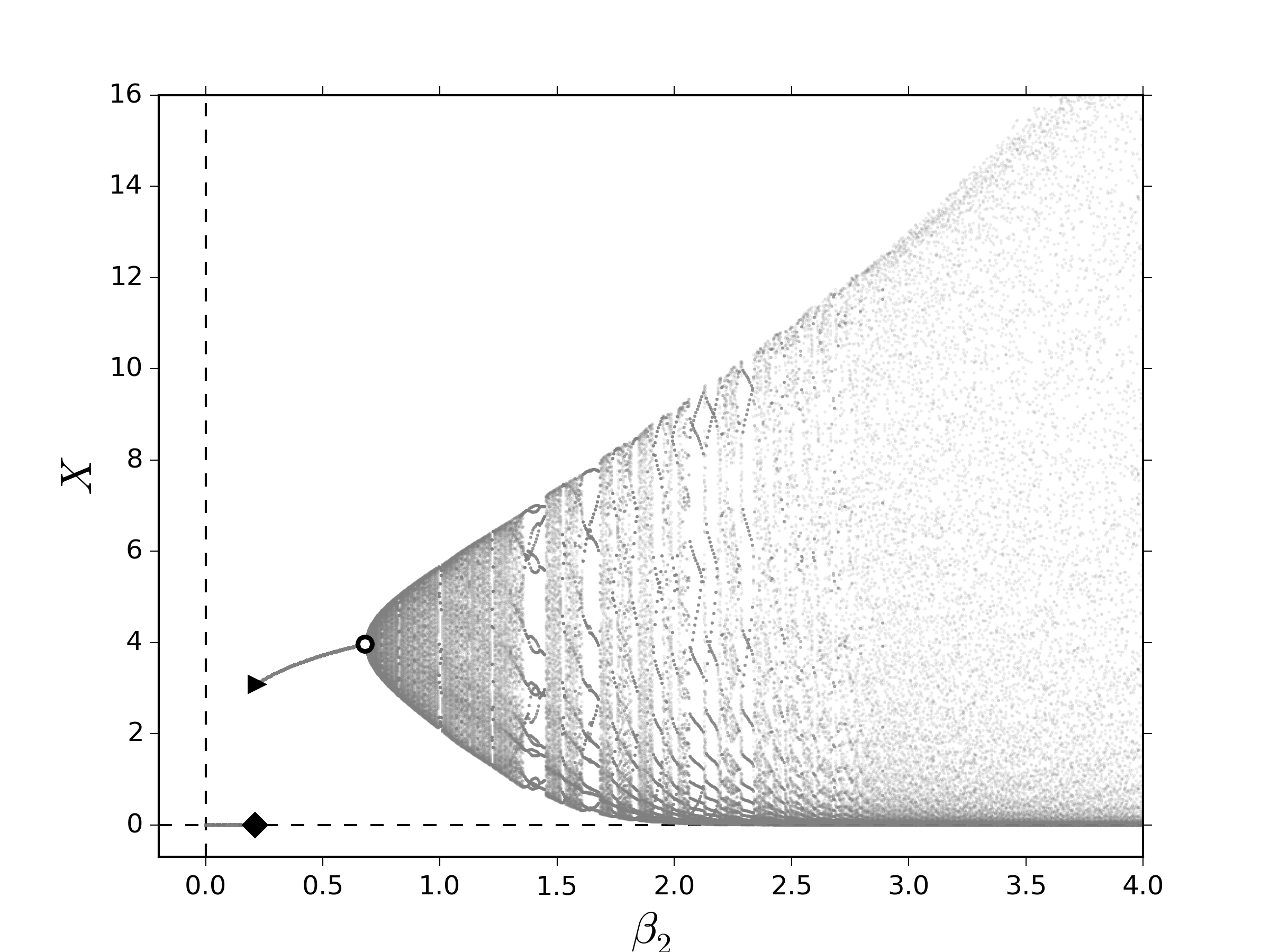
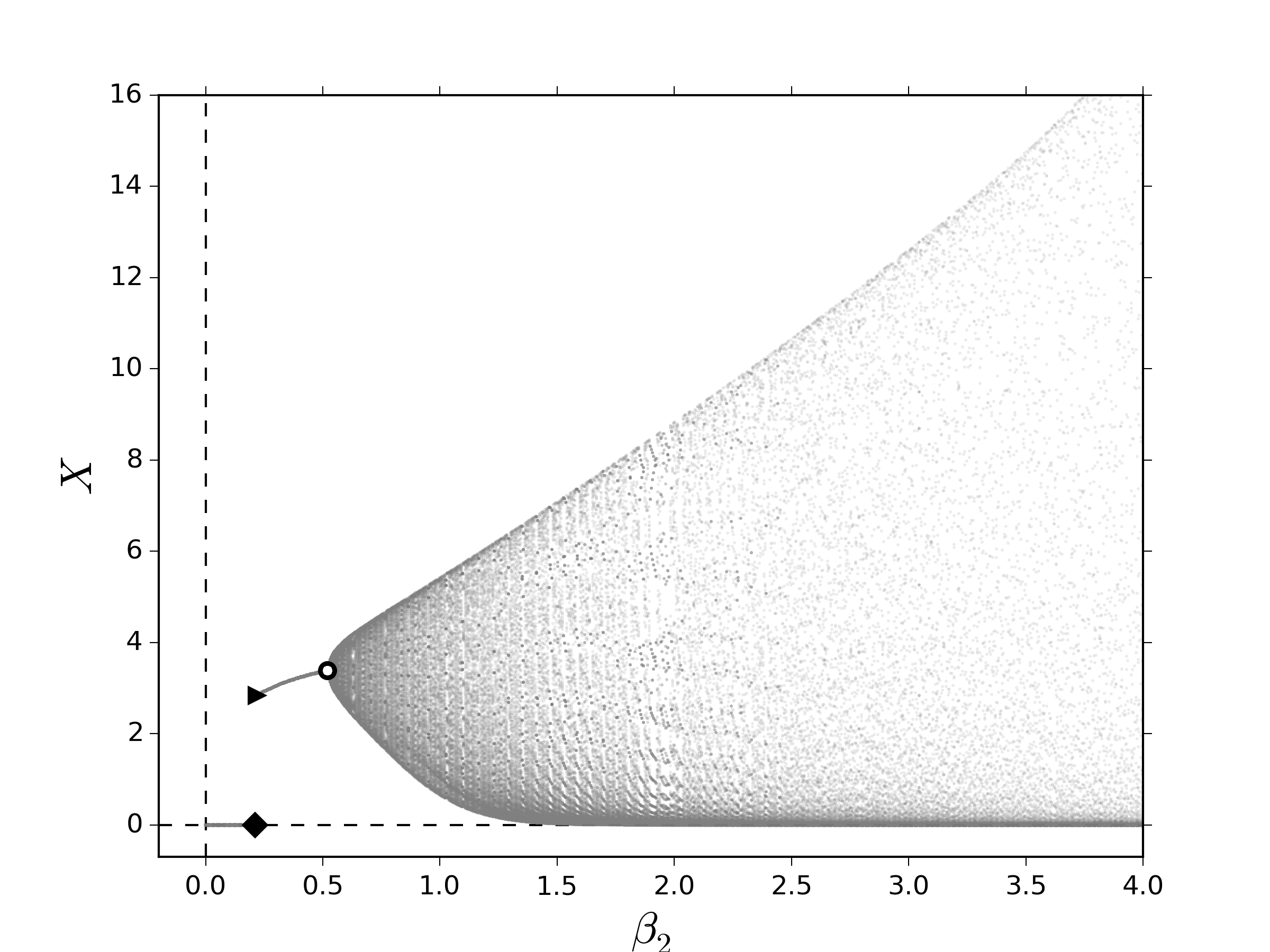
\begin{gather}\label{eq:logismod01} \psi(R_k,R_{k-1})=\frac{\tilde\gamma KR_{k-1}R_k}{\left(\tilde\gamma R_{k-1}-1\right)R_k+K}\,,\tag{12a} \end{gather} de tal modo que el sistema \eqref{eq:lesliemod} toma la forma \begin{gather}\label{eq:logismod02} \vecoldos{\vectorr{x}_{k+1}}{R_{k+1}}=\vecoldos{\vectorr{L}\left(R_k\right)\vectorr{x}_k}{f\left(R_k,R_{k-1},X_k\right)}\,.\tag{12b} \end{gather}Los puntos fijos del sistema \eqref{eq:lesliemoddelay} y, correspondientemente su estabilidad, se verán afectados por la inclusión del término de retraso. El impacto de una dinámica como ésta induce que el crecimiento de los recursos $\psi\left(R_k,R_{k-1}\right)$ en el crecimiento de los recursos por contacto con la población $f\left(R_k,R_{k-1},X_k\right)$ tiene un cambio de concavidad al variar $R_k$ en condiciones de equilibrio, es decir, esta función es sigmoide cuando $R_k=R_{k-1}$. Esto quiere decir que existe un valor crítico de los recursos, $R^*$, donde la razón de crecimiento desacelera. Dicho de otro modo, los recursos saturan el medio rápidamente cuando se satisface que $R_k\menorque R^*$ y cuando éstos sobrepasan el umbral dado por $R_k=R^*$ se obtiene el intervalo de tiempo denominado: tiempo intrínseco de saturación de los recursos. Como consecuencia dinámica, esto sugiere que no solamente los puntos fijos sufren un cambio, sino también los valores propios. Con el fin de explorar numéricamente los efectos inducidos por el retraso en la dinámica de los recursos, calculamos el diagrama de bifurcación al variar el número promedio de descendientes para la segunda clase. De igual manera que en la figura 1, la evidencia numérica mostrada en la figura 2 sugiere que al variar lentamente $\beta_2$ es posible encontrar condiciones para favorecer la aparición de puntos fijos positivos y de comportamientos cuasi-periódicos. Primero, notemos que las bifurcaciones NS ocurren en valores de $\beta_2$ menores que en los diagramas mostrados en la figura 1; sin embargo, la ventana en la cual no hay ocurren comportamientos oscilatorios y positivos, $\beta_2^{\textrm{TS}}\menorque \beta_2\menorque \beta_2^{\textrm{NS}}$, parece aumentar en el régimen de transición lenta y disminuir en el régimen de transición rápida como se muestra en la figura 2(a) y la figura 2(b), respectivamente. Además, en la figura 2(a) parece que no existen ventanas de periodicidad a diferencia de la figura 1(a). Estas observaciones sugieren que el retraso favorece el comportamiento cuasi-periódico, una vez que éste ocurre.
Una vez explorado brevemente las consecuencias de la inclusión de términos con retraso, mostramos experimentos numéricos que corresponden a una interacción por competencia entre clases.
La competencia por recursos puede deberse a alguna jerarquía, por ejemplo, determinadas por características intrínsecas a la población o, inclusive, a influencia externa. De este modo, la competencia entre especies puede considerarse como una interacción donde los individuos de algunas clases es desfavorecida por la interacción con los miembros de otras clases. En este sentido, los sistemas \eqref{eq:lesliemod} y \eqref{eq:lesliemoddelay} son modificados por un término de competencia entre clases, aquí denominado como $\vectorr{H}\left(\vectorr{x}_k\right)$. En general, obtenemos el sistema de la forma
\begin{gather}\label{eq:FullLesliemod01} \vecoldos{\vectorr{x}_{k+1}}{R_{k+1}}=\vecoldos{\vectorr{L}\left(R_k\right)\vectorr{x}_k}{f\left(R_k,R_{k-1},X_k\right)}+\boldsymbol{\eta}\vecoldos{\vectorr{H}\left(\vectorr{x}_k\right)}{0}\,,\tag{13a} \end{gather}donde $\boldsymbol{\eta}$ es la matriz de competencia entre clases.
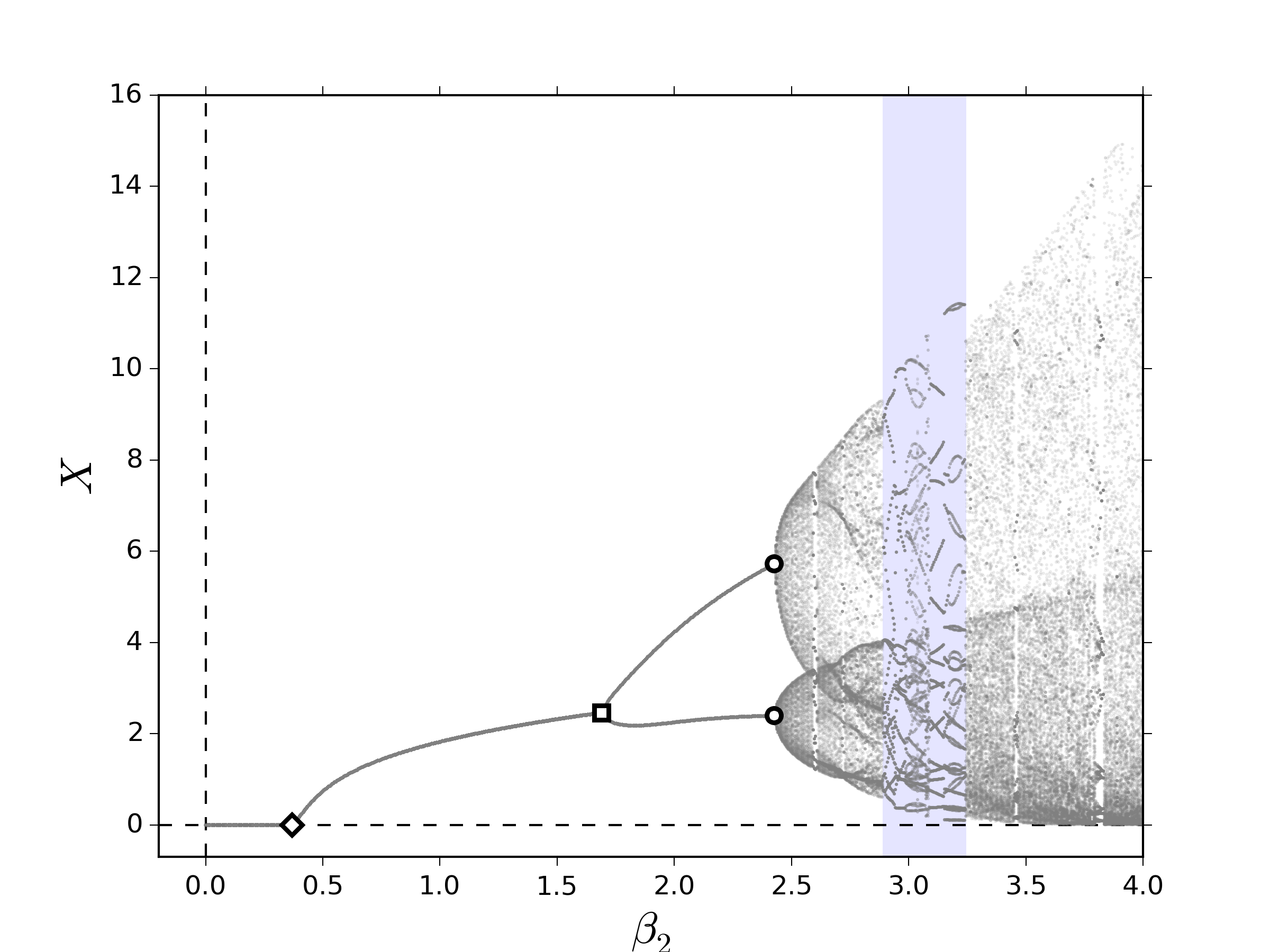
Con el fin de ilustrar el impacto que este tipo de consideraciones tienen en la dinámica no lineal del crecimiento de una población dividida por clases con términos de retraso, para fines prácticos, suponemos que la competencia por recursos ocurre entre clases dos-a-dos; de este modo, $\boldsymbol{\eta}=\diag{\eta_{ij}}$ y las componentes del término de competencia entre clases son dados por
\begin{gather}\label{eq:FullLesliemod02} \vectorr{H}(\vectorr{x}_k)_i=h\left(x_{ik}\right)x_{jk}^2\left\{\begin{array}{rl} \displaystyle 0\,, & i=1\,,\\[0.5ex] 1\,, & 1\menorque i\menorque j\,,\\[0.5ex] -1\,, & i\leq j\leq n\,, \end{array}\right. \quad \textrm{donde} \quad h\left(x_{ik}\right)=\frac{x_{ik}}{1+\omega x_{ik}}\tag{13b} \end{gather}es la función de interacción entre individuos de la $i$-ésima clase y la $j$-ésima clase, de tal manera que $\omega^{-1}$ es la máxima interacción. Asimismo, la función \eqref{eq:FullLesliemod02} captura la suposición que los miembros de la primer clase no compiten por los recursos y los individuos de las clases superiores eligen mecanismos de defensa por agregación.
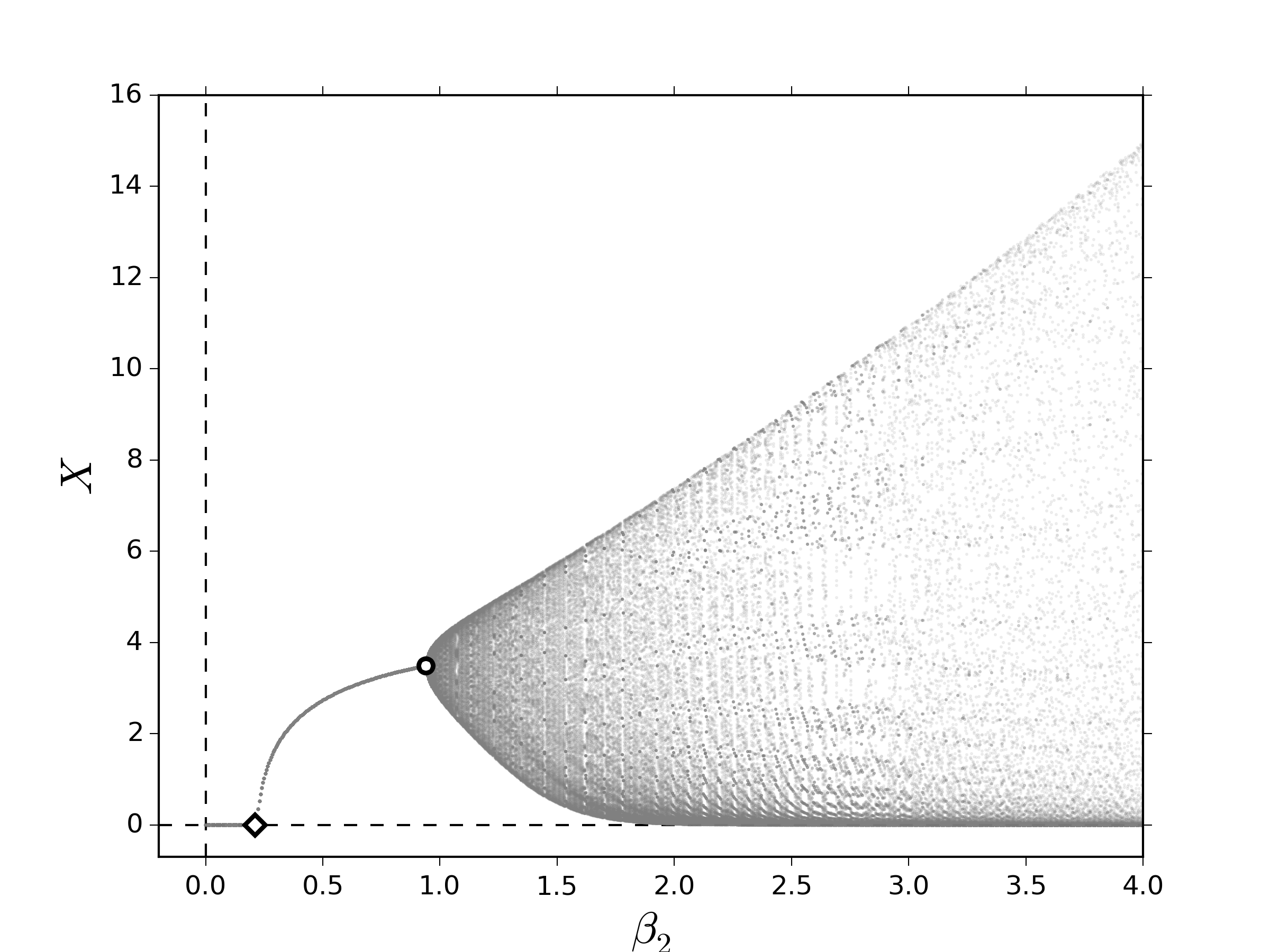
En la figura 3, pueden observarse los diagramas de bifurcación al variar lentamente $\beta_2$. Los efectos esenciales capturados por el sistema \eqref{eq:FullLesliemod} indican que, al igual que en los resultados numéricos mostrados en las figuras 1 y 2, los términos de retraso parecen favorecer la emergencia de comportamientos cuasi-periódicos, los cuales emergen a partir de una bifurcación NS. Por otro lado, los términos de competencia entre clases muestran dos características clave:
En el presente manuscrito hemos explorado superficialmente algunas incógnitas dinámicas en un modelo que captura tres características esenciales en ecología: (i) clasificación por características intrínsecas de los individuos en una población; (ii) dinámica de recursos limitados; (iii) competencia entre los miembros de la población.
Los resultados numéricos realizados sugieren que la rapidez de transición entre clases debida a la cantidad de recursos controla la emergencia de comportamientos periódicos y cuasi-periódicos. Por otro lado, los términos de competencia parecen regular la dinámica de crecimiento de la población. De esta forma, la dinámica es menos sensible a condiciones externas para valores pequeños de $\beta_2$ y, una vez en la región de los parámetros donde ocurren comportamientos cuasi-periódicos, parece desfavorecer las consecuencias de perturbaciones en el régimen de cuasi-periodicidad.
Desde la perspectiva de los sistemas dinámicos emergen distintas incógnitas que merecen ser estudiadas. Por ejemplo, la búsqueda de las condiciones que producen el cambio de criticalidad en presencia de competencia, los eventos dinámicos que otros parámetros pueden producir, el análisis que describa la emergencia de comportamientos con características caóticas. En este sentido, la investigación que puede llevarse a cabo consiste en la existencia de puntos fijos, la ruta al caos que sigue una dinámica como la que se presenta aquí, la caracterización de los comportamientos cuasi-periódicos, la búsqueda de distintos escenarios de competencia o la influencia de retrasos a distinto orden.
La columna vertebral del presente texto consiste en que el tipo de ideas teóricas utilizadas no sólo son de una simpleza fascinante, sino que abre un abanico dinámico de gran riqueza En otras palabras, no solamente el modelo captura hipótesis de especial importancia ecológica, sino que plantea problemas matemáticos que pueden abordarse con ideas básicas. Asimismo, estimula el planteamiento de líneas de estudio tanto en la ecología como en las matemáticas.